Скачать определение ускорения свободного падения, исходные файлы

Введение

Целью данной работы является измерение ускорения свободного падения с помощью математического и физического маятника, где физический маятник - тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, не проходящей через центр тяжести тела, а математический маятник может быть осуществлен в виде тяжелого груза, достаточно малых размеров, подвешенный на нити. Колебания – движения, обладающие той или иной степенью повторяемости.

Описание лабораторной установки и методики измерений

Будем измерять период и время колебания маятников, с помощью маятника универсального FPM-04. Установка состоит из: штатива, на котором подвешен маятник, фотоэлектронной пары, фиксирующей количество и время колебаний.

Принципиальная схема:

Физический (маятник - стержень)

Математический (груз на нити)

Методика измерений

Измерим длину маятника и отклонив маятник на несколько градусов, отпустим его. После 10 колебаний зафиксируем время колебаний, и повторим опыт несколько раз, меняя длину маятника

Физический маятник

Период колебаний рассчитывается по формул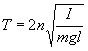е , где

I – момент инерции,

T – период колебания,

m – масса груза,

g – ускорение свободного падения,

l- длина маятника,

n – число Пи.

Формула справедлива лишь при малых амплитудных колебаниях.

Результаты

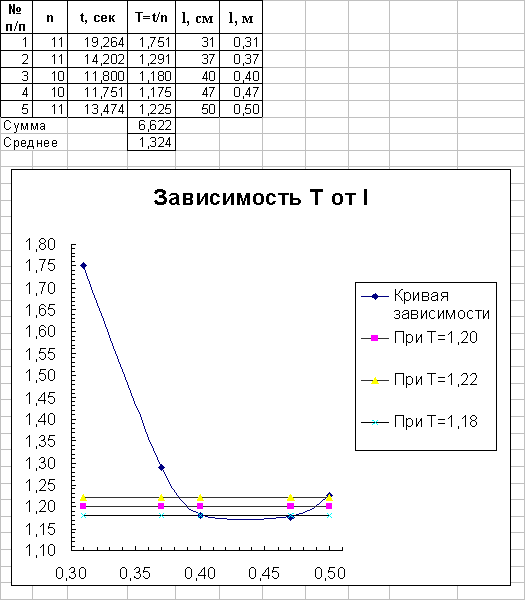
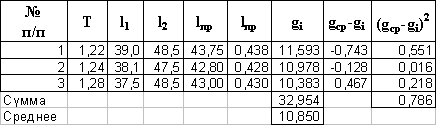
Определяем абсолютную и случайную погрешность

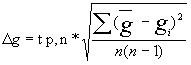= 0,34

g = 10,85 ± 0,34 м/с² p = 0,95

Определяем относительную погрешность

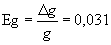
E_g = 0,031*100% = 3,1%

Математический маятник

Период колебания вычисляется по формуле .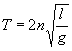

Результаты

График зависимости T от l выглядит как прямая.

Определяем абсолютную и случайную погрешность

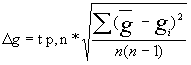= 0,177

g = 10,15 ± 0,18 м/с² p = 0,95

Определяем относительную погрешность

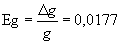
E_g = 0,018*100% = 1,8%

Вывод: выполнив данную работу ускорение свободного падения составило 10,85 м/с², при измерении с помощью физического маятника, и 10,15 м/с², при измерении с помощью математического маятника. Относительная погрешность в первом случае почти в 2 раза больше (3,1% и 1,8%). Результат отклоняется от табличного значения на 9,5% и 3,3%, измерен с достаточной точностью.

Следовательно, измерение при помощи математического маятника, в данных условиях, дает более точный результат.