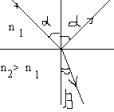
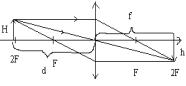
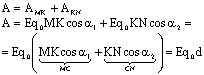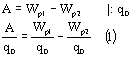Электрический заряд – это физическая величина, характеризующая электромагнитное взаимодействие. Тело заряжено отрицательно, если на нем избыток электронов, положительно – дефицит.
Перечислим свойства зарядов
1. Существуют заряды двух видов; отрицательные и положительные. Разноименные заряды притягиваются, одноименные отталкиваются. Носителем элементарного, т.е. наименьшего, отрицательного заряда является электрон, заряд которого qe= -1,6*10-19Кл, а масса mе=9,1*10-31кг. Носителем элементарного положительного заряда является протон qр=+1,6*10-19Кл, масса mр=1,67*10-27кг.
2. Электрический заряд имеет дискретную природу. Это означает, что заряд любого тела кратен заряду электрона q=Nqe, где N – целое число. Однако мы, как правило, не замечаем дискретности заряда, так как элементарный заряд очень мал.
3. В изолированной системе, т.е. в системе, тела которой не обмениваются зарядами с внешними по отношению к ней телами, алгебраическая сумма зарядов сохраняется (закон сохранения заряда).
4. Эл. заряд всегда можно передать от одного тела к другому.
5. Единица заряда в СИ – кулон (Кл). По определению, 1 кулон равен заряду, протекающему через поперечное сечение проводника за 1 с при силе тока 1 А.
6. Закон сохранения зарядов – в замкнутой системе алгебраическая сумма зарядов не изменяется. Этот экспериментально установленный факт называется законом сохранения электрического заряда. Нигде и никогда в природе не возникает и не исчезает заряд одного знака. Появление каждого положительного заряда всегда сопровождается появлением равного по абсолютному значению отрицательного заряда. Ни положительный, ни отрицательный заряд не могут исчезнуть в отдельности один от другого, они могут лишь взаимно нейтрализовать друг друга, если равны по абсолютному значению.
Взаимодействие заряженных тел
Электростатика изучает свойства и взаимодействия неподвижных в инерциальной системе отсчета электрически заряженных тел или частиц.
Самое простое явление, в котором обнаруживается факт существования и взаимодействия электрических зарядов, - это электризация тел при соприкосновении. Возьмем две полоски бумаги и проведем по ним несколько раз пластмассовой ручкой. Если взять ручку и полоску бумаги и начать их сближать, то бумажная полоска начнет изгибаться в сторону ручки, т. е. между ними возникают силы притяжения. Если взять две полоски и начать их сближать, то полоски начнут изгибаться в разные стороны, т. е. между ними возникают силы отталкивания.
Взаимодействие тел, обнаруженное в данном опыте называется электромагнитным. Физическая величина, определяющая электромагнитное взаимодействие, называется электрическим зарядом.
Способность электрических зарядов как к взаимному притяжению, так и к взаимному отталкиванию объясняется существованием двух видов зарядов: положительного и отрицательного.
Очевидно, что при соприкосновении с пластмассовой ручкой, на двух одинаковых полосках бумаги появляются электрические заряды одного знака. Эти полоски отталкиваются, - следовательно, заряды одного знака отталкиваются. Между зарядами разных знаков действуют силы притяжения.
Закон Кулона
Заряды, распределенные на телах, размеры которых значительно меньше расстояний между ними, можно называть точечными, т. к. в этом случае ни форма, ни размеры тел существенно не влияют на взаимодействия между ними.
Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Силы электростатического взаимодействия зависят от формы и размеров взаимодействующих тел и характера распределения зарядов на них.
Силы взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению абсолютных значений зарядов и обратно пропорциональна квадрату расстояния между ними:
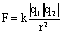
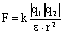
Если тела находятся в среде с диэлектрической проницаемостью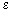 
, тогда сила взаимодействия будет ослабляться в 
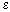раз
Силы взаимодействия двух точечных неподвижных тел направлены вдоль прямой, соединяющей эти тела.
Единицей электрического заряда в международной системе принят кулон. 1 Кл – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А.
Коэффициент пропорциональности в выражении закона кулона в системе СИ равен
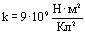
Вместо него часто используется коэффициент, называемый электрической постоянной
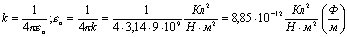
С использованием электрической постоянной закон кулона имеет вид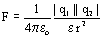 
Если имеется система точечных зарядов, то сила, действующая на каждый из них, определяется как векторная сумма сил, действующих на данный заряд со стороны всех других зарядов системы. При этом сила взаимодействия данного заряда с каким-то конкретным зарядом рассчитывается так, как будто других зарядов нет (принцип суперпрозиции).
Электрическое поле
Взаимодействие электрических зарядов объясняется тем, что вокруг каждого заряда существует электрическое поле. Электрическое поле заряда – это материальный объект, оно непрерывно в пространстве и способно действовать на другие электрические заряды. Электрическое поле неподвижных зарядов называется электростатическим. Электростатическое поле создается только электрическими зарядами, существует в пространстве, окружающем эти заряды и неразрывно с ними связано.
Электрическое поле заряда – материальный объект, оно непрерывно вы пространстве и способна действовать на другие электрические заряды. Если к электроскопу, не касаясь его оси, поднести на некотором расстоянии заряженную палочку, то стрелка все равно будет откланяться. Это и есть действие электрического поля.
Напряженность электрического поля
Заряды, находясь на некотором расстоянии один от другого, взаимодействуют. Это взаимодействие осуществляется посредством электрического поля. Наличие электрического поля можно обнаружить, помещая в различные точки пространства электрические заряды. Если на заряд в данной точке действует электрическая сила, то это означает, что в данной точке пространства существует электрическое поле. Силовой характеристикой электрического поля служит напряженностьE. Если на находящийся в некоторой точке заряд q0 действует сила F, то напряженность электрического поля Е равна: Е=F/q0. Графически силовые поля изображают силовыми линиями. Силовая линия – это линия, касательная в каждой точке которой совпадает с вектором напряженности электрического поля в этой точке.
Напряженность электрического поля – это физическая величина, численно равная силе, действующей на единичный заряд, помещенный в данную точку поля. За направление вектора напряженности принимают направление силы, действующей на точечный положительный заряд.
Однородное электрическое поле – это такое поле, во всех точках которого напряженность имеет одно и то же абсолютное значение и направление. Приблизительно однородным является электрическое поле между двумя разноименно заряженными металлическими пластинами. Силовые линии такого поля являются прямыми одинаковой густоты.
Если на заряд действуют одновременно несколько электрических полей, то напряженность поля равна векторной сумме напряженностей всех полей (принцип суперпозиции):
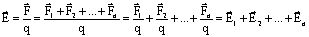
Электрическое поле точечного заряда
Рассмотрим поле точечного заряда. Напряженность этого поля в любой точке равна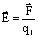 
Согласно закону Кулона 
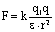Следовательно, напряженность поля точечного заряда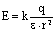 
Потенциал.
Разность потенциалов. Кроме напряженности, важной характеристикой электрического поля является потенциал j. Потенциал j - это энергетическая характеристика электрического поля, тогда как напряженность E – это его силовая характеристика, потому что потенциал равен потенциальной энергии, которой обладает единичный заряд в данной точке поля, а напряженность равна силе, с которой поле действует на этот единичный заряд.
j=Wпот/q, Здесь Wпот – потенциальная энергия заряда q в данной точке поля. Потенциал поля, созданного точечным зарядом - источником q или заряженным шаром с зарядом q, определяется формулой j=q/4pe0er. Здесь r –расстояние от точки поля с потенциалом j до точечного заряда или до центра шара. Если r=R, где R – радиус шара, то по этой формуле можно определить потенциал шара на его поверхности. Работа перемещения заряда А в электрическом поле определяется выражением A=q(j1-j2) или А=qU. Здесь j1-j2 разность потенциалов (или падение потенциала Dj, или напряжение U) между точками с потенциалами, j1 и j2. Очевидно, что если заряд перемещают между точками с одинаковыми потенциалом, то работа перемещения заряда равна нулю. Точно так же как равна нулю и работа перемещения заряда по замкнутой траектории, т.е. когда он возвращается в исходную точку с прежним потенциалом. Действительно в этом случае А=q(j1-j2)=0. в однородном электростатическом поле работа перемещения заряда q может быть определена по формуле A=Eqd, (d=Scosa), где E – напряженность этого поля, а d – проекция перемещения заряда q на силовую линию этого поля, угол между направлением перемещения S и вектором Е. Если заряд перемещается по силовой линии, то d – модуль перемещения. Если заряд перемещается перпендикулярно силовым линиям, тоa =900, соsa =0и А=0. В каждой точке однородного электрического поля напряженность одинакова по величине и направлению, а потенциал нет, так как он понижается при переходе от точек, которые ближе к положительным зарядам – источникам, к точкам, которые ближе к отрицательным зарядам источникам. В этом случае связь между разностью потенциалов j1-j2 или U и напряженностью Е выражает простое соответствие E=(j1-j2)/d или E=U/d. Следует отметить, что в электрическом поле можно отыскать точки, потенциалы которых одинаковы. Эти точки располагаются на поверхностях, перпендикулярных линиям вектора E. Такие поверхности называются эквипотенциальными. Работа перемещения заряда q вдоль эквипотенциальной поверхности равна нулю, так как A = q(j1-j2)=0. Поверхность проводника с неподвижными зарядами тоже является эквипотенциальной, поэтому при перемещении заряда по такому проводнику работы не совершается. Формулу E=(j1-j2)/d можно применять к полю бесконечной заряженной плоскости и к полю плоского конденсатора, обкладки которого заряжены разноименно (при этом если j1-j2 – разность потенциалов между обкладками, то d – расстояние между ними).
Представляет собой совокупность равных по модулю и разноименных зарядов, находящихся на малом расстоянии друг от друга. При наложении внешнего электрического поля диполи ориентируются таким образом, что поле, создаваемое поляризованным зарядом, направлено в сторону, противоположную внешнему электрическому полю. Напряженность электрического поля в диэлектрике равна разности напряжений внешнего поля Е0 и поля создаваемого поляризованным зарядом Eп: Е=Ео – Еп. В неполярных диэлектриках в отсутствие внешнего поля молекулы не являются диполями, так как центры положительных и отрицательных зарядов совпадают. При наложении внешнего электрического поля молекулы растягиваются и становятся диполями, при этом поле поляризованного заряда направлено против внешнего поля. Независимо от природы диэлектрика напряженность внешнего поля в нем всегда ослаблена в e раз: e = Ео/Е. Относительная диэлектрическая проницаемостьe показывает, во сколько раз напряженность электрического поля в диэлектрики меньше, чем в вакууме.
Диполь
(от ди... и греч. pólos - полюс) электрический, совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга. Основной характеристикой электрического Д. является его дипольный момент - вектор, направленный от отрицательного заряда к положительному (рис. 1) и численно равный произведению заряда е на расстояние l между зарядами:р = el. Дипольный момент определяет электрическое поле Д. на большом расстоянии R от Д. (R"l), а также воздействие на Д. внешнего электрического поля.
Вдали от Д. его электрическое поле Е убывает с расстоянием как 1/R3, т. е. быстрее, чем поле точечного заряда (~ 1/R2). Компоненты напряжённости поля Е вдоль оси Д. (Ep) и в направлении, перпендикулярном к р (E┴), пропорциональны дипольному моменту и в системе единиц СГС (Гаусса) равны:
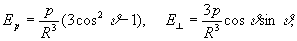
где J - угол между р и радиусом-вектором R точки пространства, в которой измеряется поле Д.; полная напряжённость
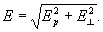
Т. о., на оси Д. при J = 0 напряжённость поля вдвое больше, чем при J = 90°; при обоих этих углах оно имеет только компоненту Ep, причём при J = 0 её направление параллельно р, а при J = 90° - антипараллельно (рис. 2).
Действие внешнего электрического поля на Д. также пропорционально величине его дипольного момента. Однородное поле создаёт вращающий момент М = pE sina (a - угол между вектором напряжённости внешнего электрического поля Е и дипольным моментом р; рис. 3), стремящийся повернуть Д. так, чтобы его дипольный момент был направлен по полю. В неоднородном электрическом поле на Д., кроме вращающего момента, действует также сила, стремящаяся втянуть Д. в область более сильного поля (рис. 4).
Электрическое поле любой нейтральной в целом системы на расстояниях, значительно больших её размеров, приближённо совпадает с полем эквивалентного Д. - электрического Д. с таким же дипольным моментом, как и у системы зарядов (т. е. поле на больших расстояниях от системы нечувствительно к деталям распределения зарядов). Поэтому во многих случаях электрический Д. является хорошим приближением для описания такой системы на больших по сравнению с её размерами расстояниях. Например, молекулы многих веществ можно приближённо рассматривать как электрический Д. (в простейшем случае это молекулы из двух ионов с зарядами противоположных знаков); атомы и молекулы во внешнем электрическом поле, несколько раздвигающем их положительные и отрицательные заряды, приобретают индуцированный (наведённый полем) дипольный момент и становятся микроскопическими Д.
Электрический Д. с изменяющимся во времени дипольным моментом (вследствие изменения его длины l или зарядов e) является источником электромагнитного излучения.
Д. магнитный. Исследование взаимодействий полюсов постоянных магнитов привело к представлению о существовании магнитных зарядов, аналогичных электрическим. Пара таких магнитных зарядов, равных по величине и противоположных по знаку, рассматривалась как магнитный Д. (обладающий магнитным дипольным моментом). Позднее было установлено, что магнитных зарядов не существует и что магнитные поля создаются движущимися электрическими зарядами, т. е. электрическими токами . Однако понятие о магнитном дипольном моменте оказалось целесообразным сохранить, поскольку на больших расстояниях от замкнутых проводников, по которым протекают токи, магнитные поля оказываются такими же, как если бы их порождали магнитные Д. (магнитное поле Д. магнитного на больших расстояниях от Д. рассчитывается по тем же формулам, что и электрическое поле Д. электрического, причём электрический момент диполя нужно заменить магнитным моментом тока). Магнитный момент системы токов определяется силой и распределением токов. В простейшем случае тока I, текущего по круговому контуру (витку) радиуса а, магнитный момент в системе СГС равен р = ISn/c, где S = pа2 - площадь витка, а единичный вектор n, проведённый из центра витка, направлен так, что с его конца ток виден текущим против часовой стрелки (рис. 5), с - скорость света.
Аналогию между магнитным Д. и витком с током можно проследить и при рассмотрении действия магнитного поля на ток. В однородном магнитном поле на виток с током действует момент сил, стремящийся ориентировать виток так, чтобы его магнитный момент был направлен по полю; в неоднородном магнитном поле такие замкнутые токи ("магнитные Д.") втягиваются в область с большей напряжённостью поля. На взаимодействии неоднородного магнитного поля с магнитным Д. основано, например, разделение частиц с различными магнитными моментами - ядер, атомов или молекул (магнитные моменты которых обусловлены движением входящих в их состав заряженных элементарных частиц, а также магнитными моментами, связанными со спинами частиц). Пучок частиц, проходя через неоднородное магнитное поле, разделяется, т.к. поле сильнее изменяет траектории частиц с большим магнитным моментом.
Однако аналогия между магнитным Д. и витком с током (теорема эквивалентности) не является полной. Так, например, в центре кругового витка напряжённость магнитного поля не только не равна напряжённости поля "эквивалентного" Д., но даже противоположна ей по направлению (рис. 6). Магнитные силовые линии (в отличие от электрических силовых линий, которые начинаются и кончаются на зарядах) являются замкнутыми.
Диэлектрики в электрическом поле
Диэлектриками или изоляторами называются тела, которые не могут проводить через себя электрические заряды. Это объясняется отсутствием в них свободных зарядов.
Если одни конец диэлектрика внести в электрическое поле, то перераспределения зарядов не произойдет, т. к. в диэлектрике нет свободных носителей заряда. Оба конца диэлектрика будут нейтральны. Притяжение незаряженного тела из диэлектрика к заряженному телу объясняется тем, что в электрическом поле происходит поляризация диэлектрика, т. е. смещение в противоположные стороны разноименных связанных зарядов, входящих в состав атомов и молекул вещества.
Полярные и неполярные диэлектрики
К неполярным относятся диэлектрики, в атомах или молекулах которых центр отрицательно заряженного электронного облака совпадает с центром положительного атомного ядра. Например, инертные газы, кислород, водород, бензол.
Полярные диэлектрики состоят из молекул, у которых центры распределения положительных и отрицательных зарядов не совпадают. Например, спирты, вода. Их молекулы можно рассматривать как совокупность двух точечных зарядов, равных по модулю и противоположных по знаку, находящихся на некотором расстоянии друг от друга. Такую в целом нейтральную систему называют электрическим диполем.
Поляризация полярных диэлектриков
При отсутствии электрического поля тепловое движение приводит к беспорядочной ориентации диполей, а в электрическом поле происходит смещение положительных зарядов в направлении электрического поля.
Поляризация неполярных диэлектриков
При отсутствии электрического поля электронное облако расположено симметрично относительно атомного ядра, а в электрическом поле оно изменяет свою форму и центр отрицательно заряженного электронного облака уже не совпадает с центром положительного атомного ядра.
В результате поляризации на поверхности вещества появляются связанные заряды, которые обуславливают взаимодействие нейтральных тел из диэлектрика с заряженными телами. Напряженность поля, создаваемого связанными зарядами на поверхности диэлектрика направлена внутри диэлектрика противоположно напряженности внешнего электрического поля, вызывающего поляризацию. Напряженность электрического поля внутри диэлектрика оказывается равной
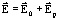или 
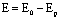, где
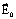- напряженность внешнего электрического поля
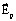- напряженность поля, создаваемого связанными зарядами
Диэлектрическая проницаемость
Диэлектрическая проницаемость вещества – это физическая величина, равная отношению модуля напряженности электрического поля в вакууме к напряженности электрического поля в однородном диэлектрике
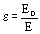
Диэлектрическая проницаемость показывает, во сколько раз диэлектрик ослабляет электрическое поле.
Проводники в электрическом поле
Проводниками называются тела, способные пропускать через себя электрические заряды. Это свойство проводников объясняется наличием в них свободных носителей заряда. Примерами проводников могут быть металлы и растворы электролитов.
Если взять металлический проводник и один его конец поместить в электрическое поле, то на данном конце появится электрический заряд. Согласно закону сохранения электрического заряда, на другом конце проводника появится равный ему по модулю и противоположный по знаку заряд. Явление разделения разноименных зарядов в проводнике, помещенном в электрическое поле, называется электростатической индукцией.
При внесении в электрическое поле проводника свободные заряды в нем приходят в движение. Перераспределение зарядов вызывает изменение электрического поля. Движение зарядов прекращается только тогда, когда напряженность электрического поля внутри проводника становится равной нулю.
Свободные заряды перестают перемещаться вдоль поверхности проводящего тела при достижении такого распределения, при котором вектор напряженности электрического поля в любой точке перпендикулярен поверхности тела. Поэтому в электрическом поле поверхность проводника любой формы является эквипотенциальной поверхностью (см. ниже).
Электростатическое поле внутри проводника равно нулю, весь статический заряд проводника сосредоточен на его поверхности.
Заряд, сообщенный проводнику, распределится по его поверхности не равномерно. Поверхностной плотностью заряда называется физическая величина, равная отношению заряда к площади, на которой он расположен:
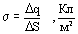
Чем больше кривизна поверхности, тем больше поверхностная плотность заряда. Заряды скапливаются на выступах или остриях.
Работа электрического поля при перемещении заряда
На пробный электрический заряд, помещенный в электростатическое поле, действует сила, заставляющая этот заряд перемещаться. Значит, эта сила совершает работу по перемещению заряда. Получим формулу для расчета работы этой силы.
Рассмотрим однородное электрическое поле (такое поле существует между пластинами плоского заряженного конденсатора вдали от его краев):
Допустим, что мы поместили пробный заряд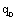 
в точку М. Тогда сила 
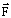во всех точках поля имеет один и тот же модуль и направление. Под действием силы заряд перемещается в точку N. Работа, совершенная полем:
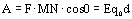
Представим, что заряд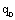 
переместился по пути MKN. Работа поля по перемещению заряда:
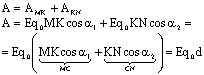
Представим, что заряд переместился из точки N в точку M по криволинейной траектории. Тогда мы можем разделить эту траекторию на малые участки, каждый из которых можно будет считать прямолинейным. Запишем работу на каждом таком участке, затем эти работы сложим и придем к тому же результату. Значит ее работа не зависит от траектории движения, а зависит только от расположения начальной и конечной точки движения. Мы рассмотрели однородное электрическое поле, но полученный вывод верен для любого электростатического поля.
Сила, работа которой не зависит от формы пути, проходимого точкой приложения силы, называется консервативной (потенциальной) силой. Следовательно, сила, действующая на заряд в электрическом поле – консервативная.
Допустим, что в некотором электростатическом поле пробный заряд q0 переместился из точки 1 в точку 2. Из механики известно, что работа консервативных сил по перемещению заряда равна убыли потенциальной энергии системы:
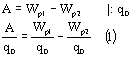
В одной точке электрического поля разные заряды могут обладать различной потенциальной энергией, но отношение потенциальной энергии к заряду для данной точки поля оказывается постоянной величиной. Она называется потенциалом и ее принимают за энергетическую характеристику данной точки поля:
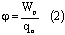
Из выражений (1) и (2) получим:
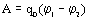
Т. е. работа, совершаемая силами электрического поля при перемещении заряда, равна произведению заряда на разность потенциалов начальной и конечной точек траектории движения заряда.
Физический смысл потенциала: Предположим, что заряд равен единице, тогда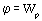 
. Таким образом, потенциал – физическая величина, численно равная той потенциальной энергии, которой обладает пробный заряд, равный единице, помещенный в данную точку поля. (Так мы говорим для краткости: на самом деле Wp – потенциальная энергия системы зарядов, образующих поле и пробного заряда, внесенного в это поле).
За единицу потенциала принимают потенциал такой точки поля, в которой пробный заряд 1 Кл обладает потенциальной энергией 1 Дж. Эта единица – 1 Вольт.
Доказано, что потенциал в некоторой точке поля, созданного точечным зарядом q рассчитывается по формуле:
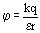(*), где
r – расстояние от заряда, образующего поле, до точки, в которой нужно найти потенциал.
Потенциал – скалярная величина. Потенциалы точек поля, созданного положительным зарядом, являются положительными величинами и наоборот. Если поле создано несколькими зарядами, то потенциал каждой точки этого поля есть алгебраическая сумма потенциалов отдельных полей.
Из формулы (*) видно, что потенциал равен нулю, в точках пространства, расположенных бесконечно далеко от заряда, образующего поле.
/*----------------------------------------------------
Можно дать другое толкование физического смысла потенциала:
Предположим, что под действием сил поля заряд переместился из точки поля 1 в бесконечно далекую точку. Тогда работа, совершенная сила ми поля:
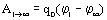. Но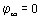 
, т. к. в бесконечно далекой точке поле отсутствует. Следовательно,
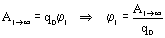
Значит, потенциал поля в точке 1 – физическая величина, численно равная работе, которую совершат силы поля, перемещая единичный заряд из данной точки поля в бесконечно далекую точку.
----------------------------------------------------*/
Значение потенциала данной точки поля зависит от выбора поверхности нулевого потенциала. В физике считают, что нулевым потенциалом обладают точки пространства, бесконечно далекие от зарядов, образующих поле. В радиотехнике считают, что нулевым потенциалом обладают точки поверхности земли. В формулу работы входит разность потенциалов, а эта величина не зависит от выбора точки нулевого потенциала.
Поверхности, перпендикулярные к силовым линиям называются эквипотенциальными поверхностями (поверхностями равного потенциала). Все точки таких поверхностей имеют одинаковый потенциал. Работа поля по перемещению заряда по эквипотенциальной поверхности равна нулю.
Разность потенциалов
Физическая величина, равная работе, которую совершат силы поля, перемещая заряд из одной точки поля в другую, называется напряжением между этими точками поля.
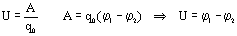
Рассмотрим однородное электростатическое поле (такое поле существует между пластинами плоского заряженного конденсатора вдали от его краев):
Во время перемещения заряда поле совершает работу:
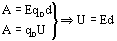
Индукция электростатическая,
наведение в проводниках или диэлектриках электрических зарядов в постоянном электрическом поле.
В проводниках подвижные заряженные частицы - электроны - перемещаются под действием внешнего электрического поля. Перемещение происходит до тех пор, пока заряд не перераспределится так, что созданное им электрическое поле внутри проводника полностью скомпенсирует внешнее поле и суммарное электрическое поле внутри проводника станет равным нулю. (Если бы этого не произошло, то внутри проводника, помещенного в постоянное электрическое поле, неограниченно долго существовал бы электрический ток, что противоречило бы закону сохранения энергии.) В результате на отдельных участках поверхности проводника (в целом нейтрального) образуются равные по величине наведённые (индуцированные) заряды противоположного знака.
В диэлектриках, помещенных в постоянное электрическое поле, происходит поляризация, которая состоит либо в небольшом смещении положительных и отрицательных зарядов внутри молекул в противоположные стороны, что приводит к образованию электрических диполей (с электрическим моментом, пропорциональным внешнему полю), либо в частичной ориентации молекул, обладающих электрическим моментом, в направлении поля. В том и другом случае электрический дипольный момент единицы объёма диэлектрика становится отличным от нуля. На поверхности диэлектрика появляются связанные заряды. Если поляризация неоднородная, то связанные заряды появляются и внутри диэлектрика. Поляризованный диэлектрик порождает электростатическое поле, добавляющееся к внешнему полю.
Электроемкость – количественная мера способности проводника удерживать заряд.
Простейшие способы разделение разноименных электрических зарядов – электризация и электростатическая индукция – позволяют получить на поверхности тел не большое количество свободных электрических зарядов. Для накопления значительных количеств разноименных электрических зарядов применяются конденсаторы.
Конденсатор – это система из двух проводников (обкладок), разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Так, например, две плоские металлические пластины, расположенные параллельно и разделенные слоем диэлектрика, образуют плоский конденсатор.
Если пластинам плоского конденсатора сообщить равные по модулю заряды противоположного знака, то напряженность электрического поля между пластинами будет в два раза больше, чем напряженность поля у одной пластины. Вне пластин напряженность электрического поля равна нулю, т. к. равные заряды разного знака на двух пластинах создают вне пластин электрические поля, напряженности которых равны по модулю, но противоположны по направлению.
Электроемкостью конденсатораназывается физическая величина, определяемая отношением заряда одной из пластин к напряжению между обкладками конденсатора:
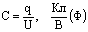
При неизменном положении пластин электроемкость конденсатора является постоянной величиной при любом заряде на пластинах.
За единицу электроемкости в системе СИ принимают Фарад. 1 Ф – электроемкость такого конденсатора, напряжение между обкладками которого равно 1 В при сообщении обкладкам разноименных зарядов по 1 Кл.
Электроемкость плоского конденсатора можно вычислить по формуле:
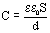, где
S – площадь обкладок конденсатора
d – расстояние между обкладками
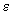– диэлектрическая проницаемость диэлектрика
Электроемкость шара можно вычислить по формуле:
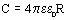
Энергия заряженного конденсатора.
Если внутри конденсатора напряженность поля E, тогда напряженность поля, созданного зарядом одной из пластин E/2. В однородном поле одной пластины находится заряд, распределенный по поверхности другой пластины. Согласно формуле для потенциальной энергии заряда в однородном поле энергия конденсатора равна:
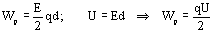
Используя формулу электроемкости конденсатора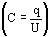 
:
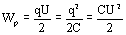
Конденсаторы.
Если изолированному проводнику сообщить заряд Dq, то его потенциал увеличиться на Dj, причем отношение Dq/Dj остается постоянным: Dq/Dj=С, где С – электрическая емкость проводника, т.е. величина, численно равная заряду, который надо сообщить проводнику, чтобы повысить его потенциал на единицу (на 1В). Электрическая емкость проводников зависит от их размеров, формы, диэлектрических свойств среды в которую они помещены, и расположения окружающих тел, но не зависит от материала проводника. В СИ за единицу электрической емкости 1 фарад (Ф): [C]=1A=1кл/1В=1А2*с4/кг*м2. Емкость равная 1Ф, очень велика, поэтому на практике чаще пользуются единицами микрофарад (1мкФ=10-6Ф) или пикофарад (1мкФ=10-12Ф). Конденсатор представляет собой систему двух проводников (обкладок) не соединенных друг с другом. Часто между обкладками помещают диэлектрик. При сообщении этим проводникам одинаковым по величине и разноименных зарядов, поле, создаваемое этими проводниками, практически полностью локализовано в пространстве между ними. Конденсаторы являются накопителями электрических зарядов. Отношение заряда на обкладке конденсатора к разности потенциалов между ними – постоянная величина: q/(j1-j2)=C.
Плоский конденсатор состоит из двух пластин площадью S, расположенных на небольшом расстоянии d друг от друга, заряды на пластинах +q и –q. В общем случае, если пространство между пластинами заполнено диэлектриком с диэлектрической проницаемостью e, то напряженность электростатического поля между пластинами равна сумме напряженности полей создаваемых каждой из пластин.
Е=s/e0e. Емкость плоского конденсатора равна С=e0eS/d.
Параллельное и последовательное соединение конденсаторов. На практике конденсаторы часто соединяют различными способами. Найти эквивалентную емкость – это значит найти конденсатор такой емкости, который при тот же разности потенциалов будет накапливать тот же заряд q, что и батарея конденсаторов. При последовательном соединении N конденсаторов заряд на обкладках одинаков, напряжение на всей батарее конденсаторов равно сумме напряжений на каждом конденсаторе в отдельности: Uобщ=U1+U2+U3+...+UN, а общая емкость N конденсаторов 1/Собщ=1/С1+1/С2+1/С3+...+1/СN. При параллельном соединении конденсаторов напряжение U на всех конденсаторах одинаково и общая емкость Собщ батареи равна сумме емкостей отдельных конденсаторов, Собщ=С1+С2+С3+...+СN.
Электрический ток
Это направленное движение заряженных частиц. В металлах носителями тока являются свободные электроны, в электролитах – отрицательные и положительные ионы, в полупроводниках – электроны и дырки, в газах – ионы и электроны. Количественной характеристикой тока является сила тока. Сила тока I определяется количеством электричества, притекающего через поперечное сечение проводника за 1 с. Если I – постоянная величина, то I=q/t, откуда следует, что за промежуток времени t через поперечное сечение проводника протекает количество электричества, равное q=It.
Источниками могут служить – гальванический элемент(происходят хим. реакции и внутренняя энергия, превращается в электрическую) и аккумулятор(для зарядки через него пропускают постоянный ток от к.-л. источника, в результате хим. реакции один электрод становиться положительно заряженным, другой – отрицательно
Действия электрического тока: тепловое, химическое, магнитное.
Направление электрического тока: от + к –
Поэтому достаточным условием для существования тока является наличие электрического поля и свободных носителей заряда.
О наличии тока можно судить по явлениям, которые его сопровождают:
- Проводник, по которому течет ток, нагревается.
- Электрический ток может изменять химический состав проводника.
- Силовое воздействие на соседние точки и намагниченные тела.
При существовании электрического поля внутри проводника, на концах его существует разность потенциалов. Если она не меняется, то в проводнике устанавливается постоянный электрический ток
Сила тока
Сила тока – отношение заряда, пронесенного через поперечное сечение проводника за интервал времени, к этому интервалу времени.
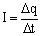
Сила тока, как и заряд, величина скалярная. Она может быть как положительной, так и отрицательной. За положительное направление силы тока принято движение положительных зарядов. Если с течением времени сила тока не меняется, то ток называется постоянным.
За единицу принимают силу тока, при которой отрезки пар. проводников длиной 1м. Взаимодействуют с силой 2*10-7 Н. Единица — 1Ампер. 1Кл=1А*1сек. Кулон равен эл. заряду, преходящему сквозь поперечное сечение проводника при силе тока 1А за время 1сек. Амперметр включают в цепь последовательно с прибором силу тока которого измеряют.
Электродвижущая сила
Для того, чтобы в проводнике существовал электрический ток длительное время, необходимо поддерживать неизменными условия, при которых возникает электрический ток.
Во внешней цепи электрические заряды движутся под действием сил электрического поля. Но, чтобы поддерживать разность потенциалов на концах внешней цепи, необходимо перемещать электрические заряды внутри источника тока против сил электрического поля. Такое перемещение может осуществляться только под действием сил неэлектростатической природы.
Силы, вызывающие перемещение электрических зарядов внутри источника постоянного тока против направления действия сил электростатического поля, называются сторонними силами. Сторонние силы в гальваническом элементе или аккумуляторе возникают в результате электрохимических процессов, происходящих на границе раздела электрод – электролит. В машине постоянного тока сторонней силой является сила Лоренца.
Полная работа сил электростатического поля при движении зарядов по замкнутой цепи постоянного тока равна нулю. Следовательно, вся работа электрического тока в замкнутой электрической цепи оказывается совершенной за счет действия сторонних сил, вызывающих разделение зарядов внутри источника и поддерживающих постоянное напряжение на выходе источника тока.
Отношение работы сторонних сил по перемещению заряда вдоль цепи называется электродвижущей силой источника:
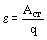
Электродвижущая сила выражается в тех же единицах, что и напряжение, т. е. в вольтах.
ЭДС численно равна работе по перемещению единичного положительного заряда. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы не консервативные (потенциальные) и их работа зависит от траектории.
Сопротивление проводников
Сопротивление является основной электрической характеристикой проводника.
Сопротивление проводника можно определить из закона Ома:
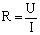
Единица электрического сопротивления в СИ – Ом. Электрическим сопротивлением 1 Обладает такой участок цепи, на котором при силе тока 1 А напряжение равно 1 В.
Опыт показывает, что электрическое сопротивление проводника прямо пропорционально его длине и обратно пропорционально площади поперечного сечения:
| 
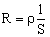
| Зависимость удельного электрического сопротивления от температуры – см. стр. 16 |
Постоянный для данного вещества параметр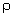 
называется удельным электрическим сопротивлением вещества. Удельное сопротивление зависит от рода вещества и его состояния (в первую очередь от температуры).
Зависимость сопротивления проводника от температуры.
Если пропустить ток от аккумулятора через стальную спираль, то амперметр покажет уменьшение силы тока. Это означает, что с сопротивлением температуры сопротивление проводника меняется.
Если при температуре, равной 0°С, сопротивление проводника равно R0, а при температуре t оно равно R, то относительное изменение сопротивления, как показывает опыт, прямо пропорционально изменению температуры t:
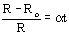(1)
Коэффициент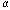 
называется температурным коэффициентом сопротивления. Он характеризует зависимость сопротивления вещества от температуры.
Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при повышении температура на 1 К.
Для всех металлов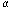 
>0 и незначительно меняется с изменением температуры. У растворов электролитов сопротивление с ростом температуры не уменьшается, а увеличивается. Для них 
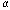<0.
При нагревании проводника его геометрические размеры меняются незначительно. Сопротивление проводника меняется в основном за счет изменения его удельного сопротивления. Можно найти зависимость этого удельного сопротивления от температуры, если в формулу (1) подставить значения
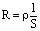и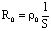 
:
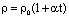
Так как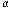 
мало меняется при изменении температуры, то можно считать, что удельное сопротивление проводника линейно зависит от температуры.
С приближением температуры к абсолютному нулю удельное сопротивление монокристаллов становится очень малым. Этот факт свидетельствует о том, что в идеальной кристаллической решетке металла электроны перемещаются под действием электрического поля, не взаимодействуя с ионами решетки. Электроны взаимодействуют лишь с ионами, не находящимися в узлах кристаллической решетки.
При повышении температуры возрастает число дефектов кристаллической решетки из-за тепловых колебаний ионов, – и это приводит к возрастанию удельного сопротивления кристалла.
Сверхпроводимость
В 1911 г. нидерландский ученый Камерлинг-Оннес обнаружил, что при понижении температуры ртути до 4,1 К ее удельное сопротивление скачком уменьшается до нуля. Явление уменьшения удельного сопротивления до нуля при температуре, отличной от абсолютного нуля, называется сверхпроводимостью. Материалы, обнаруживающие способность переходить при некоторых температурах, отличных от абсолютного нуля, в сверхпроводящее состояние, называются сверхпроводниками.
Прохождение тока в сверхпроводнике происходит без потерь энергии, поэтому однажды возбужденный в сверхпроводящем кольце электрический ток может существовать неограниченно долго без изменения.
Сверхпроводящие вещества уже используются в электромагнитах. Однако получить сколь угодно сильное магнитное поле с помощью сверхпроводящего магнита нельзя, т. к. очень сильное магнитное поле разрушает сверхпроводящее состояние. Поэтому для каждого проводника в сверхпроводящем состоянии существует критическое значение силы тока, превзойти которое, не нарушая сверхпроводящего состояния, нельзя.
Объяснение сверхпроводимости возможно только на основе квантовой теории. Оно было дано лишь в 1957 г.
В 1986 г. была открыта высокотемпературная сверхпроводимость керамик – соединений лантана, бария, меди и кислорода. Сверхпроводимость таких керамик сохраняется до температур около 100 К.
Последовательное и параллельное соединение проводников
Проводники в электрических цепях постоянного тока могут соединяться последовательно и параллельно.
При последовательном соединенииэлектрическая цепь не имеет разветвлений, все проводники включают в цепь поочередно друг за другом.
Сила тока во всех проводниках одинакова, так как в проводниках электрический заряд не накапливается и через поперечное сечение проводника за определенное время проходит один и тот же заряд:
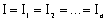
Напряжение на концах данного участка цепи складывается из напряжений на каждом проводнике:
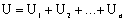(1)
По закону Ома для участка цепи:
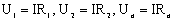и 
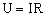(2),
где R – полное сопротивление участка цепи из последовательно соединенных проводников. Из выражений (1) и (2) получаем: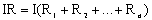 
. Таким образом:
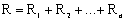
При последовательном соединении проводников их общее электрическое сопротивление равно сумме электрических сопротивлений всех проводников.
Из соотношений (2) следует, что напряжения на последовательно включенных проводниках прямо пропорциональны их сопротивлениям:
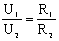
При параллельном соединении электрическая цепь имеет разветвления (точку разветвления называют узлом). Начала и концы проводников имеют общие точки подключения к источнику тока.
При этом напряжение на всех проводниках одинаково. Сила тока равна сумме сил токов во всех параллельно включенных проводниках, так как в узле электрический заряд не накапливается, поступающий за единицу времени в узел заряд равен заряду, уходящему из узла за то же время:
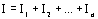(1)
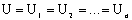
Для всех параллельно включенных проводников на основании закона Ома для участка цепи запишем:
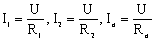(2)
Обозначив общее сопротивление участка электрической цепи через R, для силы тока в неразветвленной цепи получим
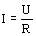(3)
Из выражений (1), (2) и (3) следует:
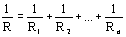
Пи параллельном соединении проводников, общая проводимость цепи равна сумме проводимостей всех параллельно соединенных проводников.
Шунтирование приборов. Сила тока в цепи измеряется амперметром. Сопротивление амперметра мало, так как он включается в цепь последовательно и не должен существенно влиять на значение силы тока в цепи. Если сила тока I в цепи больше, чем максимальное значение силы тока, которую может измерить амперметр IAmax, то к амперметру параллельно подключают шунт, так что часть тока Iш начинает течь через шунт. Для существенного увеличения диапазона измерений необходимо, чтобы сопротивлений шунта было много меньше сопротивления амперметра. Если необходимо измерить силу тока, в n раз большую, чем можно измерит данным амперметром, т.е. I/IA=n, то следует подключить шунт с сопротивлением Rш=RA/(n-1). Напряжение на различных участках цепи измеряется вольтметром, который подключается параллельно. Показания вольтметра определяются падением напряжения на сопротивлении вольтметра Uv=IvRv и равны падению напряжения на сопротивлении R. Если надо измерить напряжение больше, чем максимальное напряжение, которое может измерить данный вольтметр, то к вольтметру последовательно подключают добавочное сопротивление. Если нужно измерить напряжение в n раз большее, чем то напряжение, которое может измерить данный вольтметр, т.е. n=U/Uvmax, то необходимо подключить добавочное сопротивление Rдоб=(n-1)Rv.
Закон Ома для полной цепи
Если в результате прохождения постоянного тока в замкнутой электрической цепи происходит только нагревание проводников, то по закону сохранения энергии полная работа электрического тока в замкнутой цепи, равная работе сторонних сил источника тока, равна количеству теплоты, выделившейся на внешнем и внутреннем участках цепи:
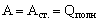(1)
По закону Джоуля – Ленца (см. ниже) количество теплоты, выделяющееся на проводнике сопротивлением R при силе тока I за время t равна:
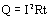
Полное количество теплоты, выделяющееся при протекании постоянного тока в замкнутой цепи, внешний и внешний и внутренний участки которого имеют сопротивления R и r, равно:
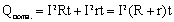(2)
Из выражений (1) и (2) получаем:
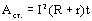, но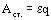 
, следовательно,
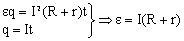
Или
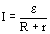- закон Ома для полной цепи.
Сила тока в полной электрической цепи прямо пропорциональна ЭДС источника тока и обратно пропорциональна полному сопротивлению цепи.
При последовательном соединении нескольких источников тока полная эдс батареи равна алгебраической сумме эдс всех источников, а суммарное сопротивление равно сумме сопротивлений. При параллельном подключении n источников с одинаковыми эдс и внутренними сопротивлениями суммарная эдс равна эдс одного источника, а внутреннее сопротивление rв=r/n. Если эдс источников различна, то для расчетов значения сил токов в различных участках цепи удобно пользоваться правилами Кирхгофа.
Первое правило Кирхгофа. Точка соединения нескольких проводников называется узлом. Алгебраическая сумма токов в узле равна нулю. Токи, идущие к узлу, будем считать положительными, от узла отрицательными. Второе правило Кирхгофа. Алгебраическая сумма падений напряжений на замкнутом контуре разветвленной цепи равна алгебраической сумме эдс.
Тепловое действие тока. Если через сопротивление R течет ток I, то кулоновские силы совершают положительную работу: A=qU=IUt, где q – количества электричества, протекшее через поперечное сечение проводника за промежуток времени t: q=It. При этом происходит выделение тепла Q. Очевидно, что Q=A, или Q=IUt=I2Rt=(U2/R)/t. (Закон Джоуля – Ленца).
правила, устанавливающие соотношения для токов и напряжений в разветвленных электрических цепях постоянного или квазистационарного тока. Сформулированы Г. Р. Кирхгофом в 1847. Первое К. п. вытекает из закона сохранения заряда и состоит в том, что алгебраическая сумма сил токов lk, сходящихся в любой точке разветвления проводников (узле), равна нулю, т. е.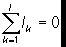 
; здесь l - число токов, сходящихся в данном узле, причём токи, притекающие к узлу, считаются положительными, а токи, вытекающие из него,- отрицательными. Второе К. и. в любом замкнутом контуре, произвольно выделенном в сложной сети проводников алгебраическая сумма всех падений напряжений lkRk на отд. участках контура равна алгебраической сумме электродвижущих сил (эдс) Ek в этом контуре, т. е.
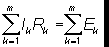
здесь m - число участков в замкнутом контуре (на рис. m = 3), Ik и Rk - сила тока и сопротивление участка номера k; при этом следует выбрать положительное направление токов и эдс, например, считать их положительными, если направление тока совпадает с направлением обхода контура по часовой стрелке, а ЭДС повышает потенциал в направлении этого обхода, и отрицательными - при противоположном направлении. Второе К. п. получается в результате применения Ома закона к различным участкам замкнутой цепи.
К. п. позволяют рассчитывать сложные электрические цепи, например, определять силу и направление тока в любой части разветвленной системы проводников, если известны сопротивления и эдс всех его участков. Для системы из n проводников, образующих r узлов, составляют n уравнений: r - 1 уравнение для узлов на основе первого К. п. (уравнение для последнего узла не является независимым, а вытекает из предыдущих) и n-(r-1) уравнений для независимых замкнутых контуров на основе второго К. п.; каждый из n проводников в эти последние уравнения должен войти хотя бы один раз. Т. к. при составлении уравнений нужно учитывать направления токов в проводниках, а они заранее не известны (и должны быть найдены из решения системы уравнений), то сначала эти направления задаются произвольно; если при решении для какого-нибудь тока получается отрицательное значение, то это означает, что его направление противоположно выбранному.
Мощность тока
Это работа, совершаемая за единицу времени и равная P=A/t=IU=I2R=U2/R. Полная мощность P0, развиваемая источником, идет на выделение тепла во внешнем и внутреннем сопротивлениях и равна P0=I2(R+r)=IE=E2(R+r). Мощность, выделяемая во внешнем сопротивлении, называется полезной мощностью и равна Pполез= E2R/(R+r)2. Мощность, выделяемая во внутреннем сопротивлении, использована быть не может и называется теряемой мощностью Ртер=I2r= E2 r /(R+r)2. Ток в электролитах. В электролитах (растворы солей, кислот, щелочей и расплавы солей ) имеются положительные и отрицательные ионы. В растворе устанавливается динамическое равновесие между процессами диссоциации и рекомбинации ионов. Под действием электрического поля ионы приобретают направленное движение – положительные ионы (катионы) движутся к катоду, отрицательные (анионы) - к аноду. При электролизе в растворах солей масса катода увеличивается, так как на катоде осаждаются положительные ионы. Например, если электролитом является раствор медного купороса, и мы берем медные электроды, то масса катода со временем увеличивается. Электролизом называется явление выделения вещества на электродах при прохождении через электролит электрического тока. Для электролиза справедливы два закона Фарадея: 1. Масса вещества, выделившегося при электролизе, прямо пропорциональна протекшему через электролит количеству электричества (заряду): m=kq=kIt, где k – электрохимический эквивалент данного вещества. Физический смысл электрохимического эквивалента состоит в следующем: k численно равен количеству вещества, выделившемуся при прохождении через электролит заряда [k] кг/Кл. 2. Второй закон Фарадея устанавливает связь между электрохимическим и химическим эквивалентом данного вещества: k=x/F, где х – химический эквивалент вещества, равный отношению атомной массы вещества А к его валентности n: x=A/n, F – постоянная Фарадея, не зависящая от свойств электролита, F=9,65*104 Кл/моль. Объединив два закона получим объединенный закон Фарадея m=(1/F)(A/n)It, т.е. масса выделившегося вещества прямо пропорциональна атомной массе, силе тока, и времени и обратно пропорциональна валентности вещества. Если выделившаяся масса вещества численно равна его химическому эквиваленту, то постоянная Фарадея численно равна заряжу, который должен пройти через электролит, чтобы на электроде выделилась масса вещества, численно равная его химическому эквиваленту.
Работа и мощность тока
Работу сил электрического поля, создающего электрический ток, называют работой тока. Работа сил электрического поля или работа тока на участке цепи с электрическим сопротивлением R за время t равна:
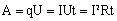
Мощность электрического тока равна работе тока за единицу времени:
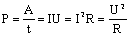
Если на участке цепи под действием электрического поля не совершается механическая работа и не происходят химические превращения веществ, то работа электрического поля приводит только к нагреванию проводника. При этом работа тока равна количеству теплоты, выделяемой проводников с током:
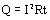
Этот закон был экспериментально установлен английским ученым Джоулем и русским ученым Ленцем, поэтому носит название Джоуля – Ленца.
Магнитное поле.
Вокруг проводников с током и постоянных магнитов существует магнитное поле. Оно возникает вокруг любого направленно движущегося электрического заряда, а также при наличии переменного во времени электрического поля. Магнитное поле можно обнаружить, помещая в него магнитные стрелки или проводники с током, так как оно оказывает на них ориентированное действие. Магнитное поле можно исследовать с помощью замкнутого контура с током. Геометрические размеры контура должны быть настолько малы, чтобы в его пределах поле не изменялось. На контур в магнитном поле действует механический вращательный момент. Отношение максимального вращательного момента Ммах к произведению силы тока I, текущего по контуру, и площади поверхности S, охватываемой этим контуром, величина постоянная: Ммах/IS=const. Этим отношением определяется основная силовая характеристика магнитного поля – вектор магнитной индукции В. Произведение IS называется магнитным моментом контура с током Pм=IS. Направление магнитного момента совпадает с направлением индукции магнитного поля, создаваемого в центре контура текущим по нему током. Направление вектора В определяется по правилу: если направление вращение винта совпадает с направлением тока в контуре, то его поступательное движение укажет направление индукции магнитного поля и, соответственно, магнитного момента (следствие правила правого винта). Итак, вектор магнитной индукции определяется максимальным вращательным моментом, действующим на контур с током, магнитный момент которого равен единице: B= Ммах/Pм. Магнитная индукция измеряется в теслах. (Тл.) Тесла – это индукция такого однородного магнитного поля, которое действует с максимальным вращательным моментом 1Н*м на контур с током, магнитный момент которого равен 1 А*м2. Индукция магнитного поля – экспериментально измеряемая величина, зависящая от токов, создающих поле, и свойств среды, в которой, в которой оно создано. Наряду с вектором магнитной индукции В вводится еще одна силовая характеристика магнитного поля – напряженность магнитного поля Н. Вектор В и Н связаны соотношением B=m0mН. Напряженность магнитного поля измеряется в амперах на метр (А/м), m0 - магнитная постоянная, равная 4p*10-7Гн/м, m - относительная магнитная проницаемость среды, показывающая, во сколько раз индукция магнитного поля в данной среде больше или меньше, чем в вакууме. Напряженность магнитного поля определяется только конфигурацией проводников, создающих поле, и токами, текущими по этим проводникам, т.е. макроисточниками поля, и не зависит от магнитных свойств среды, в которой поле создается.
Подобно тому, как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле, в пространстве, окружающем проводники с током, возникает магнитное поле. Магнитное поле представляет собой особый вид материи, посредством которого осуществляется взаимодействие между движущимися электрическими заряженными частицами.
Основные свойства магнитного поля:
· магнитное поле порождается электрическим полем.
· Магнитное поле обнаруживается по действию на ток.
· Магнитное поле материально, оно действует на тела, а следовательно, обладает энергией.
Экспериментальным доказательством реальности магнитного поля является факт существования электромагнитных волн. Сила, с которой магнитное поле действует на проводник с током, называется силой Ампера. Для характеристики способности магнитного поля оказывать силовое воздействие на проводник с током вводится векторная величина – магнитная индукция вектор В [Тл]. F=BILsin(альфа). Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют – силой Лоренца. F=B*q*V*sin(альфа).
Магнитное взаимодействие токов
Между неподвижными электрическими зарядами действуют силы, определяемые законом Кулона. Каждый заряд создает поле, которое действует на другой заряд и наоборот. Однако между электрическими зарядами могут существовать и другие силы. Их можно обнаружить если провести следующий опыт.
Возьмем два гибких проводника, укрепим их вертикально, а затем присоединим нижними концами к полюсам источника тока. Притяжения или отталкивания не обнаруживается. Но если другие концы соединить проволокой так, чтобы в проводниках возникли токи противоположного направления, то проводники начнут отталкиваться друг от друга. В случает токов одного направления проводники притягиваются.
Явление взаимодействия токов обнаружил французский физик Ампер в 1820 г. В этом же году датский физик Эрстед обнаружил, что магнитная стрелка поворачивается при пропускании электрического тока через проводник, находящийся около нее.
Взаимодействия между проводниками с током, т. е. взаимодействия между движущимися электрическими зарядами, называют магнитными. Силы, с которыми проводники с током действуют друг на друга, называют магнитными силами.
Магнитное поле
Подобно тому как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле, в пространстве, окружающем движущиеся заряды, возникает магнитное поле. Электрический ток в одном из проводников создает вокруг себя магнитное поле, которое действует на ток во втором проводнике. А поле, созданное электрическим током второго проводника, действует на первый.
Магнитное поле представляет собой особую форму материи, посредством которой осуществляется взаимодействие между движущимися электрическими заряженными частицами.
Магнитное поле создается не только электрическим током, но и постоянными магнитами. На основании своих опытов Ампер сделал вывод, что взаимодействие токов с магнитом и магнитов между собой можно объяснить, если предположить, что внутри магнита существуют незатухающие молекулярные круговые токи.
Прохождение электрического тока может сопровождаться нагреванием и свечением вещества, различными его химическими превращениями, магнитным взаимодействием. Из всех известных действий тока только магнитной взаимодействие сопровождает электрический ток при любых условиях, в любой среде и в вакууме.
Осн. задача магнитостатики состоит в умении рассчит. хар-ки полей. Закон Б-С-Л с использованием принципа суперпозиции даёт простейший метод расчёта полей.
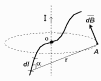
dB-индукция, созд. в точ. A.
dB=(mm0 /4p)·(I·dl·sina/r2) [1]
dH=(I·dl·sina)/(4pr2) [2]
Индукция магн. поля, созданная элементом проводника dl с током I в точке A на расстоянии r от dl пропорц. силе тока, dl, синусу угла между r и dl и обр. пропорцион. квадрату расстояния r.
___ ____ __
dB=(mm0 /4p)·(I·[dl,r] /r3)
Значение з-на Б-С-Л заключается в том, что зная dH и dB от dl можно вычислить H и B проводника конеч. размеров разл. форм.
Действие магнитного поля на движущийся заряд. Сила Лоренца
Электрический ток – это совокупность упорядоченно движущихся заряженных частиц. Поэтому действие магнитного поля на проводник с током есть результат действия поля на движущиеся заряженные частицы внутри проводника.
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца.
Модуль силы Лоренца равен отношению модуля силы Ампера, действующей на участок проводника, к числу заряженных частиц в этом участке проводника:
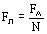
Сила Ампера равна 
, сила тока равна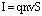 
(см. стр. 12). Подставив эти выражения в формулу для силы Лоренца, получим:
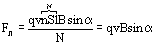
где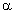 
- угол между векторами скорости и магнитной индукции.
Направление силы Лоренца определяют для положительного заряда по правилу левой руки. (Для отрицательного заряда сила Лоренца будет направлена в противоположную сторону).
Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работу. А, согласно теореме о кинетической энергии, это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.
Закон Ампера
Поместим в магнитное поле проводник длинной l, по которому течет ток I. На проводник действует сила, прямо пропорциональная силе тока, текущего по проводнику, индукции магнитного поля, длине проводника, и зависящая от ориентации проводника в магнитном поле. |F|=IBlsina, где a - угол между направлением тока в проводнике и направлением вектора магнитной индукции B, Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, что магнитные силовые линии входят в ладонь, четыре вытянутых пальца направить по току, то отогнутый большой палец укажет направление силы. Очевидно, что сила Ампера равна нулю, если проводник расположен вдоль силовых линий поля и максимальна, если проводник перпендикулярен силовым линиям. Движение заряженных частиц в магнитном поле. На проводник с током в магнитном поле действует сила Ампера FАIBlsina.Ток, в свою очередь, это направленное движение заряженных частиц. Сила тока равна I=qnvS, где q – заряд частицы, n-концентрация движущихся заряженных частиц, v-средняя скорость их направленного движения, S-площадь поперечного сечения проводника. Подставив I в выражение для FА, получим FА=qnvSBlsina, где nsl=N – общее число частиц, создающих ток. Тогда сила, действующая на отдельный движущийся заряд – сила Лоренца, равна Fл=qvBsina. где a - угол между векторами скорости и магнитной индукции. Направление силы Лоренца определяется для положительно заряженной частицы по правилу левой руки.
Закон Ампера
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
Экспериментальное изучение магнитного взаимодействия показывает, что модуль силы Ампера пропорционален длине проводника с током, силе тока и зависит от ориентации проводника в магнитном поле.
Опыт показывает, что магнитное поле, вектор индукции которого направлен вдоль проводника с током, не оказывает влияния на ток. Поэтому модуль силы зависит лишь от модуля составляющей вектора магнитной индукции, перпендикулярной проводнику.
Закон Ампера заключается в следующем. Сила Ампера равна произведению магнитной индукции поля на силу тока, длину участка проводника и на синус угла между магнитной индукцией и участком проводника:
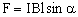
Направление силы ампера определяется по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая магнитной индукции входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 большой палец покажет направление силы, действующей на отрезок проводника.
Магнитное взаимодействие проводников с током используется в Международной системе для определения единицы сила тока –ампера.
Ампер –сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывал бы между этими проводниками силу магнитного взаимодействия, равную Н на каждый метр длины.
Магнитный поток
Магнитным потоком сквозь некоторую поверхность называют физическую величину, равную полному числу линий магнитной индукции, пронизывающих эту поверхность.
Рассмотрим однородное магнитное поле (такое поле существует внутри длинного соленоида с током вдали от его краев). Условимся рисовать линии магнитной индукции столь густо, что через единицу площади поверхности, перпендикулярную этим линиям, будет пронизываться количество линий, равное модулю магнитной индукции.
Рассмотрим плоскую прямоугольную площадку S0, перпендикулярную линиям магнитной индукции. Тогда магнитный поток Ф, пронизывающий эту поверхность, будет равен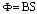 
. Рассмотрим наклонную площадку S такую, что сквозь нее проходит тот же магнитный поток, что и через S0. Из рисунка видно, что 
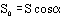. Подставим S0:
(*)
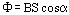Полученная формула может использоваться для расчета магнитного потока, пронизывающего наклонную плоскую площадку, расположенную в однородном магнитном поле с индукцией B. Проведем к поверхности S нормаль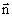 
. Эта нормаль образует с 
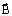также угол 
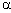(по свойству углов со взаимно перпендикулярными сторонами). Значит в формуле (*)
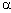– угол между 
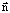и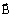 
.
Единица измерения магнитного потока – 1 Вебер. 1 Вб – это магнитный поток, пронизывающий плоскую поверхность, расположенную перпендикулярно линиям магнитной индукции в однородном магнитном поле, индукция которого равна 1 Тл.
.
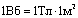В общем случае магнитное поле неоднородно, а поверхность, сквозь которую пронизываются линии магнитной индукции не является плоскостью. В этом случае мы делим всю поверхность на столь малые участки, что в пределах каждого магнитное поле можно буде считать однородным. Находим элементарные магнитные потоки, а затем их складываем.
Магнетик,
Магнитные свойства вещества
Все вещества, помещенные в магнитное поле, намагничиваются, т. е. сами создают магнитное поле. Поэтому индукция магнитного поля в однородной среде отличается от индукции поля в вакууме.
Физическая величина, показывающая, во сколько раз индукция магнитного поля в однородной среде отличается по модулю от индукции магнитного поля в вакууме, называется магнитной проницаемостью:
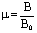
Все вещества в зависимости от их магнитной проницаемости разделяют на ферромагнетики, парамагнетики и диамагнетики.
К ферромагнетикам относятся железо, никель, кобальт и некоторые соединения этих металлов с другими элементами. У них значения магнитной проницаемости достигают тысяч единиц. Поэтому при внесении железного сердечника в катушку с током, индукция магнитного поля увеличивается во много раз.
К парамагнетикам относятся вещества, магнитная проницаемость которых немного больше единицы. (Платина, жидкий кислород)
К диамагнетикам можно отнести вещества с малой магнитной проницаемостью. Они ослабляют магнитное поле. (Серебро, свинец, кварц, висмут).
Ферромагнетизм объясняется магнитными свойствами электронов. Электрон эквивалентен круговому току или вращающемуся заряженному телу и поэтому обладает собственным магнитным полем. В большинстве кристаллов магнитные поля электронов взаимно компенсируются благодаря попарной антипараллельной ориентации магнитных полей электронов. Лишь в некоторых кристаллах, например в кристалле железа, возникают условия для параллельной ориентации собственных магнитных полей электронов. В результате этого внутри кристалла ферромагнетика возникают намагниченные области, которые называются доменами. В отдельных доменах магнитные поля имеют различные направления и в большом кристалле взаимно компенсируют друг друга. При внесении ферромагнитного образца в магнитное поле происходит упорядочение ориентации магнитных полей отдельных доменов.
С увеличением магнитной индукции внешнего поля возрастает степень упорядоченности ориентации отдельных доменов – магнитная индукция возрастает. При некотором значении индукции внешнего поля наступает полное упорядочение ориентации доменов, возрастание магнитной индукции прекращается. Это явление называется магнитным насыщением.
При вынесении ферромагнитного образца из внешнего магнитного поля значительная часть доменов сохраняет упорядоченную ориентацию – образец становится постоянным магнитом.
Упорядоченность ориентации доменов в ферромагнетике нарушается тепловыми колебаниями атомов в кристалле. Чем выше температура кристалла, тем быстрее разрушается порядок в ориентации доменов, вследствие чего образец размагничивается. Температура, выше которой вещество перестает быть ферромагнетиком, называется температурой Кюри.
Магнитный поток.
Магнитным потоком Ф через некоторую поверхность S называется скалярная величина, равная произведению модуля вектора магнитной индукции на площадь этой поверхности и косинус угла между нормалью n к ней и направлением вектора магнитной индукции B:Ф=|B|Scosa. Если магнитное поле неоднородно, то поверхность S разбивается на элементарные площадки DS в пределах каждой из которых поле можно считать однородным. Тогда полный поток через эту поверхность равен сумме потоков вектора магнитной индукции через элементарные площадки. В СИ единицей магнитного потока является 1 вебер (Вб) – магнитный поток через поверхность 1 м2, расположенную перпендикулярно направлению однородного магнитного поля, индукция которого равна 1 Тл: 1Вб=1В*с.
Электромагнитная индукция
Возникновение эдс в замкнутом проводящем контуре при изменении магнитного потока через эту поверхность, ограниченную этим контуром, называется электромагнитной индукцией. Также эдс индукции, а следовательно, разность потенциалов возникает на концах разомкнутого проводника, движущеося в магнитном поле и пересекающего силовые линии поля. Опыт показывает, что эдм индукции не зависит от причин изменния магнитного потока, а определяется скоростью его изменения. Согласно закону Фарадея, эдс индукции определяется как предел отношения изменения магнитного потока DФ к промежутку времени Dt к нулю, или производной по времени магнитного потока Eинд=limDt-->0DФ/Dt= -Ф’.
Явление электромагнитной индукции заключается в возникновении электрического тока в замкнутом электропроводящем контуре при изменении магнитного потока через площадь этого контура. По правилу Ленца, возникающий в замкнутом контуре индукционный ток направлен так, что создаваемый им магнитный поток через площадь, ограниченную контуром, стремиться препятствовать тому изменению потока, которое вызывает данный ток. Явление ЭИ находит широкое применение в технике. Оно используется в индукционных генераторах тока, индукционных плавильных печах, трансформаторах, в счетчиках электроэнергии и др.
Закон ЭИ формулируется именно для ЭДС индукции, а не для силы индукционного тока: ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром: Ei=модуль(дельта Ф/дельта t). С учетом правила Ленца: Ei=-дельта Ф/дельта t. При изменении магнитного потока в катушке, имеющей n одинаковых витков провода, общая ЭДС индукции в n раз больше ЭДС одного витка.
Индукция магнитного поля
Индукцией магнитного поля называется характеристика способности магнитного поля оказывать силовое действие на проводник с током. Она является векторной физической величиной.
За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.
Его можно определить по правилу буравчика: если направление поступательного движения буравчика совпадает с направлением силы тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции.
Линией магнитной индукции называется такая линии, в любой точке которой вектор магнитной индукции направлен по касательной.
Если во всех точках некоторой части пространства вектор индукции магнитного поля имеет одинаковое значение по модулю и одинаковое направление, то магнитной поле в этой части пространства называют однородным. Линии магнитной индукции такого поля представляют собой параллельные линии, расположенные на одном расстоянии друг от друга.
Линии индукции магнитного поля прямого проводника с током представляют собой окружности, лежащие в плоскостях, перпендикулярных проводнику. Центры окружностей лежат на оси проводника. Направление индукции в этом случае определяется следующим правилом: если смотреть вдоль проводника с током по направлению тока, то вектор магнитной индукции направлен по ходу часовой стрелки.
Линии индукции магнитного поля, созданного катушкой с током показаны на рисунке. Вектор индукции входит в катушку с той стороны, с какой направление тока в витках катушки представляется соответствующим ходу часовой стрелки.
Линии магнитной индукции не имеют ни начала, ни конца –они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Следовательно, магнитное поле –вихревое. Это позволяет сделать вывод, что магнитное поле не имеет источников. Магнитных зарядов, подобных электрическим, в природе нет.
Опытным путем установлено, что отношение максимального значения модуля силы, действующей на проводник с током (силы Ампера) к силе тока и к длине проводника, не зависит ни от силы в проводнике, ни от длины проводника. Его приняли за характеристику магнитного поля в том месте, где расположен проводник –индукцию магнитного поля:
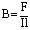
Единица индукции в этом случае определяется как индукция такого магнитного поля, в котором на 1 м проводника при силе тока 1 А действует сила Ампера 1 Н. Эта единица называется тесла:
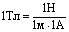
Если исследовать магнитное поле с помощью рамки с током, то модуль вектора магнитной индукции равен отношению момента сил, действующих на рамку с током со стороны поля, к произведению силы тока в рамке на ее площадь:
.
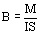За единицу магнитной индукции принята магнитная индукция такого поля, в котором на контур площадью 1 м2 при силе тока 1 А действует со стороны поля максимальный момент сил 1 .
Индукция магнитного поля зависит от геометрической формы проводника. Модуль индукции поля, создаваемого бесконечным прямолинейным проводником:
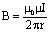, где r –расстояние от проводника.
Модуль индукции поля, созданного проводником в форме кругового витка радиуса R:
.
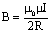Модуль индукции поля, созданного соленоидом длиной l и числом витков N:
.
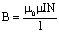Во всех формулах: I –сила тока,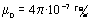 
–магнитная постоянная, 
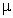– относительная магнитная проницаемость среды.
Электромагнитная индукция
Если электрический ток создает магнитное поле, то не может ли в свою очередь магнитное поле вызывать электрический ток в проводнике? Первым нашел ответ на этот вопрос Майкл Фарадей.
В 1831 г. он обнаружил, что в проводящем контуре при изменении магнитного поля возникает электрический ток, который назвали индукционным током.
Индукционный ток в катушке из металлической проволоки возникает при вдвигании магнита внутрь катушки и при выдвигании магнита из катушки, а также при изменении силы тока во второй катушке, магнитное поле которой пронизывает первую катушку. Индукционный ток также возникает при движении контура в постоянном магнитном поле.
Явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного поля, пронизывающего контур, называется электромагнитной индукцией.
Появление электрического тока в замкнутом контуре при изменениях магнитного поля, пронизывающего контур, свидетельствует о действии в контуре сторонних сил неэлектростатической природы или возникновении ЭДС индукции. Для определения ЭДС индукции введем физическую величину – магнитный поток.
Закон электромагнитной индукции
Экспериментальное исследование зависимости ЭДС индукции от изменения магнитного потока привело к установлению закона электромагнитной индукции:
ЭДС индукции в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром. С учетом правила Ленца закон электромагнитной индукции записывается следующим образом:
.
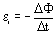Если в последовательно соединенных контурах происходят одинаковые изменения магнитного потока, то ЭДС индукции в них равна сумме ЭДС индукции в каждом из контуров. Поэтому при изменении магнитного потока в катушке, состоящей из n одинаковых витков провода, общая ЭДС индукции в n раз больше ЭДС индукции в одиночном контуре:
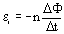
На основе закона электромагнитной индукции в Международной системе единиц определяются единицы магнитного потока и индукции магнитного поля. Магнитный поток через площадь, ограниченную замкнутым контуром, равен 1 Вб, если при равномерном убывании этого потока до нуля за 1 с в контуре возникает ЭДС индукции 1 В:
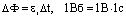
Для однородного магнитного поля на основании формулы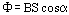 
следует, что его магнитная индукция равна 1 Тл, если магнитный поток через контур площадью 1 м2 равен 1 Вб:
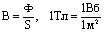
Возникновение электрического тока в замкнутом контуре свидетельствует о том, что при изменении магнитного потока, пронизывающего контур, на свободные электрические заряды в контуре действуют силы. Провод контура неподвижен, неподвижными можно считать свободные электрические заряды в нем. На неподвижные электрические заряды может действовать только электрическое поле. Следовательно, при любом изменении магнитного поля в окружающем пространстве возникает электрическое поле. Это электрическое поле и приводит в движение свободные электрические заряды в контуре, создавая индукционный электрический ток. Электрическое поле, возникающее при изменениях магнитного поля, называют вихревым электрическим полем.
Работа сил вихревого поля по перемещению электрических зарядов и является работой сторонних сил, т. е. источником ЭДС индукции. При перемещении единичного положительного заряда вдоль замкнутого неподвижного проводника она численно равна ЭДС индукции в этом проводнике.
Вихревое электрическое поле отличается от электростатического тем, что оно не связано с электрическими зарядами, его линии напряженности представляют собой замкнутые линии. Работа сил вихревого электрического поля при движении электрического заряда по замкнутой линии может быть отлична от нуля.
Рассмотрим причину возникновения ЭДС индукции в проводниках, движущих в неизменном магнитном поле. В этом случае магнитный поток через контур меняется за счет движения проводников контура. Причиной возникновения ЭДС индукции является не вихревое электрическое поле, а сила Лоренца.
Явление самоиндукции
Ток, текущий по проводящему контуру, создает вокруг него магнитное поле. Магнитный поток Ф, сцепленный с контуром, прямопропорционален силе тока в этом контуре: Ф=LI, где L – индуктивность контура. Индуктивность проводника зависит от его формы, размеров, а также от свойств окружающей среды. Так как индукционный ток вызван изменением силы тока в самом проводнике, то данное явление возникновения индукционного тока называется самоиндукцией, а возникающая эдс – эдс самоиндукции. Самоиндукция является частным случаем явления электромагнитной индукции. Если I изменяется со временем по линейному закону, то Ecи = - (DФ/Dt)= - L(DI/Dt), где DI/Dt – скорость изменения силы тока. Эта формула справедлива только при L=const. Индуктивность – величина, численно равная эдс самоиндукции, возникающей в контуре при изменении силы тока в нем на единицу за единицу времени. В СИ за единицу индуктивности принимают индуктивность такого проводника, в котором при изменении тока на 1А за 1с возникает эдс самоиндукции 1В. Эта единица называется Генри (Гн): 1Гн=1В*с/А.
Энергия магнитного поля, созданного током, по закону сохранения энергии равна энергии, затраченной источником на создание тока. При замыкании цепи ток в в цепи вследствии самоиндукции не мразу достигнет максимального значения I0, а посепенно. При размакании цепи ток также изчезает не сразу, а постепенно, при этом в проводнике выделяется тепло. Так как цепь разомкнута, то это тепло не может выделятся за счет работы источника, а может быть только следствием энергии, накопленной в соленоиде, энергии магнитного поля. Энергия магнитного поля соленоида, когда ток полностью прекратиться, переходит в джоулево тепло. Выражение для магнитного поля соленоида имеет вид: Wм=LI2/2.
Явление самоиндукции. Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток через контур из этого проводника пропорционален модулю индукции магнитного поля внутри контура, а индукция магнитного поля в свою очередь пропорциональна силе тока в проводнике. Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
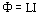
Коэффициент пропорциональности между силой тока в контуре и магнитным потоком, создаваемым этим током, называется индуктивностью. Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
За единицу индуктивности в Международной системе принимается генри. Индуктивность контура равна 1 Гн, если при силе тока 1 А магнитный поток через контур равен 1 Вб:
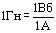
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного поля, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке. Явление возникновения ЭДС индукции в электрической цепи в результате изменения силы тока в этой цепи называется самоиндукцией.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
ЭДС самоиндукции, возникающая в катушке, по закону электромагнитной индукции равна
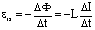, т. е.
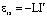
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Элемент электрической цепи обладает индуктивностью 1 Гн, если при равномерном изменении силы тока в цепи на 1 А за 1 с в нем возникает ЭДС самоиндукции 1 В.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Энергию магнитного поля катушки индуктивности можно вычислить следующим способом. Для упрощения расчета рассмотрим такой случай, когда после отключения катушки от источника ток в цепи убывает со временем по линейному закону. В этом случае ЭДС самоиндукции имеет постоянное значение, равное
,
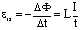где t – промежуток времени, за который сила тока в цепи убывает от начального значения I до 0.
За время t при линейном убывании силы тока от I до 0 в цепи проходит электрический заряд:
,
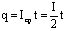поэтому работа электрического тока равна
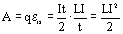
Эта работа совершается за счет энергии магнитного поля катушки. Энергия магнитного поля катушки индуктивности равна половине произведения ее индуктивности на квадрат силы тока в ней:
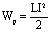
Электромагнитные волны.
Согласно теории Максвелла, переменное магнитное поле вызывает появление переменного вихревого эл. поля, которое, в свою очередь, вызывает появление переменного магнитного поля и т.д. Таким образом происходит распространение электромагнитных возмущений в пространстве т.е. распространяется электромагнитная волна. Основные свойства электромагнитных волн. 1. Электромагнитная волна – поперечная. 2. Скорость электромагнитных волн в вакууме равна v=c=3*108м/с и совпадает со скоростью света. В среде v=c/Ö(em), где e и m - диэлектрическая и магнитная проницаемости среды. 3. Электромагнитные волны переносят энергию. 4. Электромагнитные волны отражаются от проводящих поверхностей и преломляются на границе двух диэлектриков. 5. Электромагнитные волны оказывают давление на тела. 6. Если электромагнитная волна оказывает давление на тела, т.е. сообщает им импульс, следовательно, она также обладает импульсом. 7. Наблюдается дифракция, интерференция и поляризация электромагнитных волн.
Шкала электромагнитных волн.
Электромагнитные волны генерируются в широком диапазоне частот. Каждый участок спектра имеет свое названия. Так, видимому свету соответствует довольно узкий диапазон часто и соответственно длин волн: от 4*10-7 до 7,5*107. С коротковолновой стороны от видимой области спектра находиться ультрафиолетовая область, с длинноволновой - инфракрасная. За ультрафиолетовым диапазоном идет рентгеновский, а затем g-излучение. g-лучи – электромагнитное излучение самой большой частоты n³1020 Гц (l~10-12м). Радиоволны лежат в диапазоне l>10-2м.
Задача создания источника когерентного света была решена лишь с появлением Л., в котором используется принципиально иной метод высвечивания возбуждённых атомов, позволяющий, несмотря на некогерентный характер возбуждения отдельных атомов, получать когерентные пучки света с очень малой расходимостью. Если интенсивность излучения Л. сравнить с интенсивностью излучения абсолютно чёрного тела в том же спектральном и угловом интервалах, то получаются фантастически большие температуры, в миллиарды и более раз превышающие реально достижимые температуры тепловых источников света. Кроме того, малая расходимость излучения позволяет с помощью обычных оптических систем концентрировать световую энергию в ничтожно малых объёмах, создавая громадные плотности энергии. Когерентность и направленность излучения открывают принципиально новые возможности использования световых пучков там, где нелазерные источники света неприменимы.
Принцип работы лазера. Возбуждённый атом может самопроизвольно (спонтанно) перейти на один из нижележащих уровней энергии, излучив при этом квант света. Световые волны, излучаемые нагретыми телами, формируются именно в результате таких спонтанных переходов атомов и молекул. Спонтанное излучение различных атомов некогерентно. Однако, помимо спонтанного испускания, существуют излучательные акты др. рода. При распространении в среде световой волны с частотой v, соответствующей разности каких-либо двух энергетических уровней E1, E2 атомов или молекул среды (hn = E2 - E1, где h - Планка постоянная), к спонтанному испусканию частиц добавляются др. радиационные процессы. Атомы, находящиеся на нижнем энергетическом уровне E1, в результате поглощения квантов света с энергией hn переходят на уровень E2 (рис. 2, а). Число таких переходов пропорционально r (n) N1, где r (n) - спектральная плотность излучения в эрг/см3, N1 - концентрация атомов, находящихся на уровне E1 (населённость уровня). Атомы, находящиеся на верхнем энергетическом уровне E2, под действием квантов hn вынужденно переходят на уровень E1 (рис. 2, б). Число таких переходов пропорционально r (n) N2, где N2 - концентрация атомов на уровне E2. В результате переходов E1 ° E2 волна теряет энергию, ослабляется. В результате же переходов E2 ° E1 световая волна усиливается. Результирующее изменение энергии световой волны определяется разностью (N2 - N1). В условиях термодинамического равновесия населённость нижнего уровня N1 всегда больше населённости верхнего N2. Поэтому волна теряет больше энергии, чем приобретает, т. е. имеет место поглощение света. Однако в некоторых специальных случаях оказывается возможным создать такие условия, когда возникает инверсия населённостей уровней E1 и E2, при которой N2 > N1. При этом вынужденные переходы E2 ° E1 преобладают и поставляют в световую волну больше энергии, чем теряется в результате переходов E1 ° E2. Световая волна в этом случае не ослабляется, а усиливается.
Излучаемые атомами в результате вынужденных переходов E2 ° E1 волны по частоте n, направлению распространения, поляризации и фазе тождественны первичной волне и, следовательно, когерентны друг другу независимо от того, каким образом происходило возбуждение атомов на уровень E 2. Именно когерентность вынужденного излучения приводит к усилению световой волны в среде с инверсией населённостей, а не просто к дополнительному излучению новых волн. Среду с инверсией населённостей какой-либо пары уровней E1, E2, способную усиливать излучение частоты n = (E2 - E1)/h, обычно называют активной.
Спонтанное излучение одного из возбуждённых атомов активной среды (т. е. атома, находящегося на уровне E2), прежде чем оно выйдет из объёма V, может вызвать вынужденные переходы др. возбуждённых атомов и вследствие этого усилится (рис. 3). Существенно, что усиление зависит от пути, проходимого волной в среде, т. е. от направления. Если поместить активную среду в простейший оптический резонатор, т. е. между двумя параллельными полупрозрачными зеркалами, находящимися на определённом расстоянии друг от друга, как в интерферометре Фабри - Перо (рис. 4), то в наиболее благоприятные условия попадает волна, распространяющаяся вдоль оси интерферометра. Усиливаясь, она достигнет зеркала, отразится от него и пойдёт в обратном направлении, продолжая усиливаться, затем отразится от второго зеркала и т.д. При каждом "проходе" интенсивность волны увеличивается в ekL раз, где k - коэффициент усиления в см-1, L - длина пути волны в активной среде. Если усиление на длине L больше потерь, испытываемых волной при отражении, то с каждым проходом волна будет усиливаться всё больше и больше, пока плотность энергии r (n) в волне не достигнет некоторого предельного значения. Рост r (n) прекращается, когда выделяемая в результате вынужденных переходов энергия, пропорциональная r (n), не может компенсироваться энергией, затрачиваемой на возбуждение атомов. В результате между зеркалами устанавливается стоячая волна, а сквозь полупрозрачные зеркала выходит наружу поток когерентного излучения.
Интерферометр Фабри - Перо, заполненный активной средой с достаточно большим коэффициентом усиления, представляет собой простейший Л. В Л. используются оптические резонаторы и др. типов - с плоскими зеркалами, сферическими, комбинациями плоских и сферических и др. (см. Открытый резонатор). В оптических резонаторах, обеспечивающих обратную связь в Л., могут возбуждаться только некоторые определённые типы колебаний электромагнитного поля, называются собственными колебаниями или модами резонатора. Моды характеризуются частотой и формой, т. е. пространственным распределением колебаний. В резонаторе с плоскими зеркалами (рис. 4) преимущественно возбуждаются типы колебаний, соответствующие плоским волнам, распространяющимся вдоль оси резонатора. Такой резонатор позволяет получать излучение высокой направленности. Телесный угол DW, в котором сосредоточен поток излучения, может быть сделан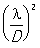 
, где D - диаметр зеркал. Для l " 1 мкм и D = 1 см величина 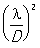" 10-8 (для тепловых источников DW ~ 2p).
Оптический резонатор накладывает ограничения на спектральный состав излучения. При заданной длине резонатора L в нём возбуждаются волны с частотами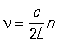 
, где с - скорость света, n - целое число. В результате спектр излучения Л., как правило, представляет собой набор узких спектральных линий, интервалы между которыми одинаковы и равны c/2L. Число линий (компонент) при заданной длине L зависит от свойств активной среды, т. е. от спектра спонтанного излучения на используемом квантовом переходе и может достигать нескольких десятков и сотен (рис. 5). При определённых условиях оказывается возможным выделить одну спектральную компоненту, т. е. осуществить одномодовый режим генерации. Спектральная ширина каждой из компонент dnл определяется потерями энергии в резонаторе и, в первую очередь, пропусканием и поглощением света зеркалами. Так как величина dnл может быть сделана во много раз меньше ширины спектральных линий спонтанного излучения атомов, то излучение Л. в одномодовом режиме характеризуется высокой монохроматичностью.
Существующие Л. различаются: 1) способом создания в среде инверсии населённостей, или, как говорят, способом накачки (оптическая накачка, возбуждение электронным ударом, химическая накачка и т.п.; см. ниже); 2) рабочей средой (твёрдые диэлектрики, полупроводники, газы, жидкости); 3) конструкцией резонатора; 4) режимом работы (импульсный, непрерывный). Все эти различия определяются потребностями применений, предъявляющих часто совершенно различные требования к характеристикам Л.
Методы создания инверсии населённости. Для создания активной Среды необходимо избирательное возбуждение атомов, обеспечивающее преимущественное заселение одного или нескольких уровней энергии. Одним из наиболее простых и эффективных методов является метод оптической накачки, который был использован в первом Л. на рубине. Рубин представляет собой кристалл окиси алюминия Al2O3 с примесью (~ 0,05%) ионов Cr3+, замещающих атомы Al (см. Рубин). Уровни энергии иона Cr3+ в рубине показаны на рис. 6. Поглощение света, соответствующего синей и зелёной областям спектра, переводит ионы Cr3+ с основного уровня E1 на возбуждённые уровни, образующие две широкие полосы 1 и 2. Затем за сравнительно малое время (~ 10-8 сек) осуществляется безызлучательный переход этих ионов на уровни E2 и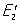 
. Избыток энергии при этом передаётся колебаниям кристаллической решётки. Время жизни ионов Cr3+ на уровнях E 2 и 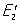составляет 10-3 сек. Только по истечении этого времени ионы снова возвращаются на основной уровень E1. Переходам E2° E1 и 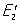° E1 соответствует излучение в красной области спектра. Если освещать кристалл рубина светом источника, обладающего достаточно большой интенсивностью в синей и зелёной областях спектра (полосы накачки), то происходит накопление ионов Cr3+ на уровнях E2 и 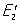и возникает инверсия населённостей этих уровней по отношению к осн. уровню E1. Это позволило создать Л., работающий на переходах E2° E1 и 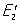° E1, генерирующий свет с длиной волны l " 0,7 мкм.
Для создания инверсии населённостей уровней E2, 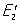относительно E1 необходимо перевести больше половины ионов Cr3+ на уровни E2, 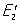за время, не превышающее 10-3 сек. Это предъявляет большие требования к мощности источника накачки. В качестве таких источников используются импульсные ксеноновые лампы. Длительность импульса накачки обычно ~ 10-3 сек. За это время в каждом см3 кристалла поглощается энергия в несколько дж.
Метод оптической накачки обладает несколькими преимуществами. Во-первых, он применим для возбуждения сред с большой концентрацией частиц (твёрдые тела, жидкости). Во-вторых, этот метод возбуждения весьма селективен. Так, в рубине в основном поглощается только та часть спектра излучения ламп накачки, которая ответственна за возбуждение ионов Cr3+. Всё остальное излучение попадает в область прозрачности и поглощается относительно слабо. Поэтому отношение полной энергии, вложенной в единицу объёма рабочего вещества, к полезной энергии, затраченной на создание инверсной населённостей уровней, в основном определяется особенностями используемой системы уровней. Все остальные потери энергии сведены к минимуму. В рубине теряется лишь та часть энергии, которая идёт на возбуждение собственных колебаний кристаллической решётки в результате безызлучательных переходов (рис. 6, волнистые стрелки). Уменьшение паразитных потерь энергии существенно для уменьшения тепловых нагрузок вещества. Удельная энергия импульса генерации в твердотельных Л. достигает нескольких дж от каждого см3 вещества. Примерно столько же энергии остаётся в рабочем веществе. Для одноатомного газа при атмосферном давлении энергия в 1 дж соответствует температуре 10000 К. Для твёрдого тела, вследствие его большой теплоёмкости, выделение энергии ~ 1 дж/см3 даёт нагрев на десятки градусов. Недостатком метода оптич. накачки является малый кпд. Отношение энергии импульса Л. к электрической энергии питания лампы-накачки в лучшем случае не превышает нескольких % из-за неполного использования спектра ламп накачки (~ 15%) и вследствие потерь на преобразование электрической энергии в световую в самих лампах.
Большое распространение получил метод создания активной среды непосредственно в электрическом разряде в различных газах. Возможности получения с помощью этого метода импульсов генерации большой энергии ограничиваются в основном малой плотностью рабочей среды; инверсию населённостей легче получить в сравнительно разреженных газах. Однако этот метод позволяет использовать в качестве активной среды Л. самые различные атомные и молекулярные газы и их смеси, а также различные типы электрических разрядов в газах. В результате оказалось возможным создать Л., работающие в инфракрасной, видимой и ультрафиолетовой областях спектра. Кроме того, возбуждение в электрическом разряде позволяет реализовать непрерывный режим работы Л. с большим кпд преобразования электрической энергии в энергию излучения Л. (см. Газовый лазер).
В наиболее мощном газоразрядном Л. непрерывного действия на смеси молекулярных газов CO2 и N2 (с добавлением ряда др. компонентов) механизм образования инверсии населённостей состоит в следующем: электроны газоразрядной плазмы, ускоряемые электрическим полем, при столкновениях возбуждают колебания молекул N2. Затем в результате столкновений возбуждённых молекул N2 с молекулами CO2 происходит заселение одного из колебательных уровней CO2, что и обеспечивает возникновение инверсии населённостей. Все стадии этого процесса оказываются очень эффективными, и кпд достигает 20-30%.
В дальнейшем оказалось возможным создать газодинамический лазер на смеси CO2 и N2, в котором газовая смесь нагревается до температуры Т ~ 2000 К, формируется сверхзвуковой поток, который, выходя из сопла, расширяется и тем самым быстро охлаждается. В результате быстрого охлаждения возникает инверсия населённостей рабочих уровней CO2 (см. Газодинамический лазер). Кпд преобразования тепловой энергии в излучение газодинамического Л. невелик (~ 1%). Тем не менее газодинамические Л. весьма перспективны, т. к., во-первых, в этом случае облегчается задача создания крупногабаритных Л. большой мощности и, во-вторых, при использовании тепловых источников энергии вопрос о кпд Л. стоит менее остро, чем в случае электроразрядных Л. При сжигании 1 г топлива (например, керосина) выделяется энергия порядка десятка тыс. дж, в то время как электрическая энергия, запасаемая в конденсаторах, питающих лампы вспышки, - порядка 0,1 дж на 1 см3 объёма конденсатора.
Т. к. химические связи молекул являются исключительно энергоёмким накопителем энергии, то перспективно непосредственное использование энергии химических связей для возбуждения частиц, т. е. создание активной среды Л. в результате химических реакций. Примером химической накачки является реакция водорода или дейтерия с фтором. Если в смеси H2 и F2 к.-л. образом диссоциировать небольшое кол-во молекул F2, то возникает цепная реакция F + H2 ° HF + H, H + F2 ° HF + F и т.д. Молекулы HF, образующиеся в результате этой реакции, находятся в возбуждённом состоянии, причём для ряда квантовых переходов выполняются условия инверсии населённостей. Если к исходной смеси добавить CO2, то, кроме Л. на переходах HF (l ~ 3 мкм), удаётся также создать Л. на переходах СО2 (l = 10,6 мкм). Здесь колебательно возбуждённые молекулы HF играют ту же роль, что и молекулы N2 в газоразрядных лазерах на CO2. Более эффективной в этом случае оказывается смесь D2, F2 и CO2. В этой смеси коэффициент преобразования химической энергии в энергию когерентного излучения может достигать 15%. Химические Л. могут работать как в импульсном, так и в непрерывном режимах; разработаны различные варианты химических Л., в том числе сходные с газодинамическими Л.
Твердотельные лазеры. Существует большое количество твердотельных Л., как импульсных, так и непрерывных. Наибольшее распространение среди импульсных получили Л. на рубине (см. выше) и неодимовом стекле (стекле с примесью Nd). Неодимовый Л. работает на длине волны l = 1,06 мкм. Оказалось возможным изготовлять сравнительно большие и достаточно оптически однородные стержни длиной до 100 см и диаметром 4-5 см. Один такой стержень способен дать импульс генерации с энергией 1000 дж за время ~ 10-3 сек.
Л. на рубине, наряду с Л. на неодимовом стекле, являются наиболее мощными импульсными Л. Полная энергия импульса генерации достигает сотен дж при длительности импульса 10-3 сек. Оказалось также возможным реализовать режим генерации импульсов с большой частотой повторения (до нескольких кгц).
Примером твердотельных Л. непрерывного действия являются Л. на флюорите кальция CaF2 с примесью диспрозия Dy и Л. на иттриево-алюминиевом гранате Y3Al5O12 с примесями различных редкоземельных атомов. Большинство таких Л. работает в области длин волн l от 1 до 3 мкм. Возможность реализации непрерывного режима в этих Л. обычно связана с тем, что нижним уровнем рабочего перехода является не основной уровень E1, а возбуждённый уровень E2 (рис. 7). Если уровень E2 достаточно далеко отстоит по энергии от основного уровня E1 (по сравнению с кТ, где к - Больцмана постоянная, Т - температура) и характеризуется достаточно малым временем жизни, то инверсия населённостей для уровней E2, E3 может быть создана с помощью сравнительно маломощных источников оптической накачки. У некоторых из таких Л. генерация осуществлена при накачке солнечным светом. Типичное значение мощности генерации твердотельных Л. в непрерывном режиме ~ 1 вт или долей вт, для Л. на иттриево-алюминиевом гранате ~ десятков вт. Если не принимать специальных мер, то спектр генерации твердотельных Л. сравнительно широк, т.к. обычно реализуется многомодовой режим генерации. Однако введением в оптический резонатор селектирующих элементов удаётся получать и одномодовую генерацию. Как правило, это связано со значительным уменьшением генерируемой мощности.
Трудности выращивания больших монокристаллов или варки больших образцов однородного и прозрачного стекла привели к созданию жидкостных Л., в которых примеси атомов редкоземельных элементов вводятся не в кристаллы, а в жидкость. Однако жидкостные Л. имеют недостатки и поэтому применяются не столь широко, как твердотельные Л. (см. Жидкостный лазер).
Генерация коротких и сверхкоротких импульсов. Если для накачки твердотельного Л. используется лампа-вспышка с длительностью импульса Dtn ~ 10-3 сек, то импульс генерации длится примерно такое же время. Небольшое запаздывание начала генерации по сравнению с лампой-вспышкой обусловлено тем, что для развития генерации необходимо превысить некоторое пороговое значение инверсии населённостей, после чего усиление за один проход рабочего объёма начинает превышать суммарные потери энергии за счёт отражения луча от зеркал резонатора, паразитного поглощения и рассеяния света. При достаточно больших мощностях накачки порог генерации достигается за время t << tн. Такой режим работы Л., когда длительность лазерного импульса Dtл " Dtн, наз. режимом свободной генерации. Для ряда применений важно сократить длительность импульса Dtл, т.к. при заданной энергии импульса пиковая мощность Л. возрастает с уменьшением его длительности. С этой целью разработан метод модулированной добротности (модулируется добротность резонатора), состоящий в следующем: предварительно производят оптическую накачку, искусственно препятствуя возникновению генерации. Это осуществляют, например, помещая внутри резонатора оптический затвор. При закрытом затворе генерация невозможна, и энергия накапливается в резонаторе в виде нарастающего количества возбуждённых атомов. Если затем быстро открыть затвор, то вся запасённая энергия возбуждения, или большая её часть высвечивается в виде короткого светового импульса. Длительность такого лазерного импульса Dtл определяется или скоростью открывания затвора или, если эта скорость достаточно велика, временем установления электромагнитного поля в резонаторе.
Новые возможности сокращения длительности импульса Л. открыло применение в качестве затворов просветляющихся фильтров. Таким фильтром обычно служит слабый раствор красителя, причём концентрация поглощающей компоненты подбирается таким образом, чтобы при достаточно большой интенсивности света достигалось насыщение (см. Насыщения эффект), при этом раствор становится прозрачным (просветляется). Введение в резонатор такого фильтра повышает порог генерации: при включении накачки в рабочем объёме начинают накапливаться возбуждённые частицы; растет также и интенсивность их спонтанного излучения. Пока эта интенсивность (с учётом усиления за один проход рабочего объёма) меньше просветляющей, поглощение в фильтре препятствует развитию генерации. Но как только достигается уровень просветления, затвор автоматически выключается, и уже ничто не препятствует развитию генерации. Применение просветляющихся фильтров позволило получить гигантские импульсы света длительностью до 10-9 сек, с энергией ~ десятков дж, что соответствует мощности ~ 1010 вт.
Если обеспечивается одномодовой режим генерации, то наблюдается единый, не имеющий структуры гигантский импульс. В остальных случаях гигантские импульсы имеют сложную структуру. Например, для неодимового Л. они представляют собой последовательность значительно более коротких импульсов длительностями ~ 10-11-10-12 сек. Происхождение этой структуры объясняется следующим образом: спонтанное излучение атомов Nd в стекле характеризуется довольно широким спектром Dn ~ 1012 гц (Dl ~ 100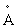
), т. е. представляет собой сумму большого числа монохроматических колебаний с частотами в интервале Dn и произвольными фазами. Поэтому интенсивность излучения изменяется во времени случайным образом (рис. 8), причём характерный временной масштаб всей этой картины, т. е. длительность типичных всплесков интенсивности, имеет порядок величины 
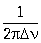. Оказалось, что с помощью введения в резонатор нелинейного элемента, каким является просветляющийся фильтр, можно сфазировать моды лазера. В идеальном случае, когда сфазированы все моды, излучение лазера приобретает вид регулярной последовательности импульсов с длительностью 
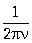. Интервалы между импульсами определяются длиной резонатора, т. е. равны периоду 2L/c. Подобный метод получения сверхкоротких и исключительно мощных импульсов получил название метода самосинхронизации мод. Практически сфазировать все моды лазера довольно трудно. Чаще всего удаётся сфазировать лишь часть из них. При этом картина формирования сверхкоротких импульсов усложняется. Реальный процесс формирования сверхкоротких импульсов с помощью просветляющегося фильтра протекает примерно следующим образом: на начальной стадии развития генерации излучение представляет собой случайный процесс. Если просветляющая интенсивность соответствует горизонтальной прямой (рис. 8), то фильтр будет выключаться теми пучками, интенсивность которых больше просветляющей. После прохождения каждого из таких пучков фильтр снова начинает поглощать. Естественно, что генерация может развиваться таким образом лишь в случае достаточно малой инерционности фильтра. Иначе после каждого сильного пика фильтр пропустит ещё несколько последующих более слабых пиков.
Просветляющийся фильтр можно подобрать так, что он будет выключаться только самыми сильными всплесками интенсивности. Это позволяет, используя некоторые дополнительные устройства, выделять отдельные сверхкороткие импульсы генерации (рис. 9). Энергия каждого из таких импульсов, как правило, невелика, однако её можно значительно увеличить, если усилить первоначальный импульс с помощью второго Л. или нескольких Л., работающих в режиме усиления и отличающихся от Л. в режиме генерации отсутствием зеркал или каких-либо др. отражающих элементов, образующих резонатор. Все возможные причины отражений устраняются выбором соответствующей конструкции. Техника формирования сверхкоротких импульсов и их последующее усиление позволяют получить импульсы генерации длительностью ~ 10-11 - 10-12 сек и пиковой мощностью ~ 1012 - 1013 вт.
Газовые лазеры. Основным достоинством газов как активной среды Л. является высокая оптическая однородность. Поэтому для тех научных и технических применений, для которых прежде всего необходимы максимально высокая направленность и монохроматичность излучения, газовые Л. представляют наибольший интерес. Вслед за первым газовым Л. на смеси гелия и неона (1960) было создано большое количество разнообразных газовых Л., в которых используются квантовые переходы нейтральных атомов, молекул и ионов, имеющих частоты в диапазоне от ультрафиолетовой до далёкой инфракрасной частей спектра. Так, Л. на водороде работает на длине волны l = 0,17 мкм, Л. на ионах Ne3+ и Ne2+ работают на длине волны l = 0,2358 мкм и l = 0,3324 мкм, а Л. на молекулах воды H2O - на длинах волн l = 27,9 мкм и l = 118,6 мкм.
Среди Л. непрерывного действия видимой и ближней инфракрасной областей спектра наибольшее распространение получил гелий-неоновый Л. Этот Л. представляет собой заключённую в оптический резонатор газоразрядную трубку, заполненную смесью Не и Ne. Он генерирует излучение с l = 0,6328 мкм, т. е. в красной области спектра. Типичные размеры трубки: длина несколько десятков см или 1-2 м; диаметр несколько мм. Мощность генерации обычно составляет десятки мвт. Гелий-неоновый Л. может работать также на целом ряде переходов в ближней инфракрасной области, например на длинах волн l = 1,152 мкм и l = 3,39 мкм. В Л. сравнительно просто реализуется предельно малая, т. е. дифракционная расходимость светового пучка.
Наиболее мощным Л. непрерывного действия в видимой области спектра является аргоновый Л. В нём используется электрический разряд в Ar с большой плотностью тока (до нескольких тысяч а/см2). Он работает на квантовых переходах иона Ar в синей и зелёной областях спектра: l = 0,4880 мкм и l = 0,5145 мкм. Мощность генерации составляет десятки вт. Конструктивно аргоновый Л. значительно сложнее гелий-неонового (необходимы охлаждение и циркуляция газа). Наиболее мощным газовым Л. является Л. на CO2 (l = 1,06 мкм). При непрерывном режиме работы СО2-Л. достигается мощность в десятки квт.
Создано также большое число импульсных газовых Л., работающих, как правило, в переходном режиме формирования разряда. Некоторые из них в режиме коротких импульсов (длительностью ~ 10-9 сек) дают сравнительно высокие пиковые мощности ~ 10 квт. СО3-Л. также может работать в импульсном режиме, обеспечивая мощность 1010 вт.
Газовые Л. способны обеспечить значительно более высокую монохроматичность излучения, нежели Л. всех др. типов. Однако на пути повышения монохроматичности и стабильности частоты излучения Л. возникает целый ряд трудностей как технического, так и принципиального характера. Различные помехи, приводящие к "качанию" частоты Л., можно разделить на два класса: технические, влияющие на собственные частоты резонатора, и физические, сказывающиеся на частоте рабочего перехода. К первым можно отнести дрожание зеркал резонатора, изменение его длины вследствие теплового расширения и т.п. Ко вторым относятся влияние внешних электрических и магнитных полей, флуктуации свойств активной среды и мощности накачки. Для уменьшения роли большинства из этих факторов имеются соответствующие методы защиты. Например, разрабатываются специальные методы автоматической подстройки резонаторов, использующие магнитострикционные явления и т.п. В основе этих методов лежит следящая система, которая фиксирует изменение параметров резонаторови обеспечивает соответствующую компенсацию. Наиболее важным фактором, лимитирующим стабильность частоты Л., являются флуктуации давления в рабочем объёме. Форма спектральной линии в газе зависит от давления, т.к. столкновения атомов и молекул в газе приводят к уширению и сдвигу спектральных линий, пропорциональным давлению. Флуктуации давления приводят к флуктуациям частоты рабочего квантового перехода. Поэтому активный газ должен находиться при возможно более низком давлении. С другой стороны, понижение давления приводит к уменьшению коэффициента усиления среды. Это противоречие частично удаётся разрешить методом стабилизации частоты излучения Л. с помощью поглощающей ячейки, помещаемой в резонатор. В поглощающей ячейке находится газ, имеющий спектральную линию поглощения, перекрывающую линию, соответствующую рабочему переходу активной среды. Например, у гелий-неонового Л. для линии l = 3,39 мкм таким газом является метан CH4. Оказалось возможным стабилизировать частоту излучения Л. по частоте линии поглощения метана, причём в условиях, когда давление поглощающего газа значительно меньше активного. С помощью поглощающей ячейки достигнута относительная стабильность частоты излучения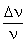 
~ 10-13 - 10-14.
Полупроводниковые лазеры. Среди Л. видимого и инфракрасного диапазонов полупроводниковые Л. занимают особое положение по ряду своих характеристик. В полупроводниках удаётся получить очень большие коэффициенты усиления ~ 102 - 103 см-1, поэтому размеры полупроводникового Л. могут быть сделаны очень малыми - порядка долей мм. Л. на полупроводниках GaAs, CdS, InAs, InSb, ZnS и др. позволяют почти полностью перекрыть видимый и ближний инфракрасный диапазоны. Полупроводниковые инжекционные лазеры характеризуются очень высоким кпд преобразования электрической энергии в когерентное излучение (близким к 100%) и могут работать в непрерывном режиме. При температуре жидкого гелия достигается мощность ~ 10 вт, при температуре жидкого азота 4-5 вт. Особенно перспективные инжекционные Л. на гетеропереходах, которые работают в непрерывном режиме при комнатной температуре, создавая мощность ~5×10-2 вт при кпд до 25%.
В полупроводниковых Л. с возбуждением электронным пучком можно возбуждать большие объёмы полупроводников, чем в случае инжекции через р - n-переходы. Пиковая мощность при этом доходит до 1 Мвт при средней мощности ~ 1 вт. Кпд при электронном возбуждении не может превышать 30%.
Общим недостатком всех полупроводниковых Л. является сравнительно невысокая направленность излучения, связанная с их малыми размерами, и трудность получения высокой монохроматичности. Последнее связано с большой шириной спектра спонтанного излучения на рабочих рекомбинационных переходах.
Полупроводниковые Л. используются с наибольшей эффективностью в тех случаях, когда требования к когерентности и направленности не очень велики, но необходимы малые габариты и высокий кпд. Полупроводниковые Л. превосходят Л. всех остальных типов плотностью энергии излучения и величиной кпд. Важным качеством полупроводниковых Л. является возможность перестройки частоты излучения и управления световым пучком, т. е. модуляция интенсивности света с постоянной времени ~ 10-11 сек.
Применение лазеров. Одновременно с созданием первых Л. начали развиваться различные направления их применений. Создание Л. ликвидировало качественное отличие оптики от радиоэлектроники. Т. о., все радиотехнические методы принципиально могут быть осуществлены и в оптическом диапазоне, причём малость длины волны лазерного излучения открывает ряд дополнительных перспектив. Л. большой мощности позволяют изучать разнообразные явления при взаимодействии света большой интенсивности со средой, ранее совершенно недоступные для эксперимента. В исследованиях молекулярного рассеяния света лазерные источники значительно расширили возможности экспериментальной техники, в частности позволили исследовать свойства жидкого и твёрдого гелия (затухания второго звука, связанные состояния двух ротонов в жидком гелии и т.п.), провести первые исследования кинетики движения некоторых биологических объектов, например простейших бактерий. С помощью коротких и сверхкоротких импульсов можно изучать чрезвычайно быстрые релаксационные процессы в конденсированных средах с временем релаксации ~ 10-13 сек. Возможность формировать сверхкороткие импульсы света 10-11 - 10-12 сек имеет также очень важное значение для скоростной фотографии и ряда др. методов исследования быстропротекающих процессов. С помощью гелий-неонового Л., обладающего высокой стабильностью частоты, возможно создание единого оптического стандарта длины (длина волны) и времени (частота). Для измерения абсолютного значения частоты гелий-неонового Л. (3,32 мкм) эта частота после преобразования измеряется в ед. частоты клистрона (0,074230 1012 гц). Это позволяет получить наиболее точное значение скорости света с = 2,99792456,2 + 1,1 м/сек.
Исключительно высокая эффективная температура излучения Л. и возможность концентрировать энергию в ничтожно малом объёме открыли уникальные возможности испарения и нагрева вещества. Важнейшей задачей является нагрев плазмы до температур, достаточных для осуществления термоядерных реакций, т. е. получения термоядерной плазмы. Достигнуты температуры 20×106 К. В тех же условиях эксперимента, при соответствующем подборе химического состава испаряемой мишени, удаётся получить точечный источник рентгеновского излучения высокой интенсивности (мощностью ~109 вт при длительности импульса в несколько нсек). Существует возможность создания интенсивных точечных источников нейтронов. Нагрев плазмы лазерным лучом оказался эффективным методом получения многозарядных ионов различных элементов. Впервые в лабораторных условиях получены и исследованы спектры ряда многозарядных ионов, представляющих интерес для астрофизики .
Мощные Л. начали применяться и в технологии. С их помощью возможны сварка, закалка, резка и сверление различных материалов без возникновения в них механических напряжений, неизбежных при обычной обработке, и с очень большой точностью, вплоть до нескольких длин волн. Обрабатываются материалы любой твёрдости, металлы, алмазы, рубины и т.п. Л. начинают применяться при резке газовых труб и т.п.
Большие возможности открываются перед лазерной техникой в биологии и медицине. Лазерный луч применяется не только в хирургии (например, при операциях на сетчатке глаза) как скальпель, но и в терапии.
Интенсивно развиваются методы лазерной локации и связи. Локация Луны с помощью рубиновых Л. и спец. уголковых отражателей, доставленных на Луну, позволила увеличить точность измерения расстояний Земля - Луна до нескольких см. Полная затрата энергии при этом порядка энергии, выделяющейся при сгорании десятка спичек. С помощью полупроводникового Л. осуществлена связь со спутником. Разрабатываются лазерные методы геодезических измерений и регистрации сейсмических явлений. Созданы и используются лазерные гироскопы и дальномеры.
Большое внимание уделяется созданию Л. с перестраиваемой частотой. Существуют различные типы параметрических генераторов света: Л. на вынужденном рассеянии света и полупроводниковые Л., работающие в одномодовом режиме. В результате перекрыт практически весь диапазон от l = 1 мм до видимой области, причём обеспечивается разрешение 10-2-10-3 см-1. Широкое применение подобных Л. в спектроскопии позволит во многих случаях исключить необходимость в монохроматорах, спектрографах и т.п. Особенно большое значение лазерная спектроскопия должна иметь для исследования короткоживущих продуктов, исследования химических реакций, биологических превращений и т.п.
Получены обнадёживающие результаты в направленном стимулировании химических реакций. С помощью Л. можно селективно возбуждать одно из собственных колебаний молекулы. Оказалось, что при этом молекулы способны вступать в реакции, которые нельзя или затруднительно стимулировать обычным нагревом. Для реализации всех имеющихся здесь возможностей необходимы мощные Л. с перестраиваемой частотой в ближней инфракрасной области спектра.
Новые методы получения инверсии населённости (разряд с принудительной ионизацией) позволили поднять давление в активной среде молекулярных газовых Л. до 10-20 am. При таких давлениях колебательно-вращательные уровни молекул перекрываются вследствие столкновений, что открывает новые возможности перестройки частоты Л.
30. Поляризациясвета
Это явление наложения волн с образованием устойчивой картины максимумов и минимумов. При интерференции света на экране наблюдается чередование светлых и темных полос, если свет монохроматический (излучаются электромагнитные волны одной длины), или цветных полос, если цвет белый или состоит из волн разной длинны. Необходимым условием наблюдения интерференционной картины является когерентность волн. Два различных источника света не могут быть когерентны. Свет излучается возбужденными атомами, время излучения атома длится ~10-8с, период колебаний, возбуждаемых световой волной ~10-15с. Невозможно согласовать излучение двух атомов одного источника, тем более, невозможно согласовать излучение двух разных источников. Каждый атом излучает короткий цуг волн, который можно представить как сумму монохроматических волн с начальной фазой, определяемой моментом излучения. Поэтому интерферировать могут лишь волны, испускаемые в одном и том же акте излучения. Для получения интерференционной картины видимого света необходимо разделить излучения от одного источника на два потока, эти потоки направить по двум разным траекториям, а затем соединить их в некоторой области пространства. В этом случае в данной точке пространства будут сходиться волны, испущенные одним атомом в одном акте излучения, и разность фаз колебаний, возбуждаемых в этой точке этими волнами, будет определятся только разностью хода волн. Например, луч, падающий непосредственно на экран SA, и луч, отразившийся от зеркала, ОА, будут когерентны. Разность геометрических волн в данном случае является разностью хода волн D=(SO+OA)-SA. Очевидно, что разность хода волн не должна превышать 3 м. Если D>3 м, то в точке A встречаются волны, излученные разными атомами, так как за время 10-8с одним атомом излучается цуг волн длиной l=ct=3 м, где с – скорость света, равная 300000 км/с.
Возможность наблюдения И. с. зависит от степени монохроматичности света. В белом свете можно наблюдать только несколько интерференционных полос вблизи D = 0, которые в этом случае окрашены, потому что положение максимумов и минимумов зависит от длины волны. Если из источника света выделена одна узкая спектральная линия, максимальная разность хода Dmax может достигать нескольких десятков см. Чёткие интерференционные полосы ещё можно наблюдать при Dmax " l2/Dl, где Dl - ширина спектра. Dmax можно связать со временем t, в течение которого фаза волны не сбивается, т. е. излучается волна в виде отрезка синусоиды ("цуг волн"). При этом Dmax оказывается равной длине цуга: Dmax = l2/Dl = ct (c - скорость света), что поясняет невозможность И. с. при D > Dmax, так как соответствующие цуги в двух интерферирующих пучках перестают перекрываться друг другом.
Ограничения размеров источника в приведённых выше опытах снимаются, если источником света служит излучение лазера, которое обладает пространственной когерентностью, и И. с. может наблюдаться при сложении волн, испускаемых разными точками источника. Высокая монохроматичность лазерного излучения позволяет наблюдать И. с. при огромной разности хода.
При очень малых интенсивностях света, когда при помощи чувствительных приёмников регистрируются отдельные фотоны, И. с. проявляется как статистическое явление. Среднее число квантов, попавших на тот или другой участок экрана в течение определённого времени, даёт такое же распределение интенсивности, что и при обычном способе наблюдения. Это находится в полном соответствии с квантовой теорией, согласно которой И. с. происходит не в результате сложения разных фотонов, а в результате "интерференции фотона самого с собой".
Интерференцию поляризованных лучей широко используют в кристаллооптике для определения структуры и ориентации осей кристалла, в минералогии для определения минералов и горных пород, для обнаружения и исследования напряжений и деформаций в твёрдых телах, для создания особо узкополосных светофильтров и др.
Явление огибания волнами препятствий и попадания света в область геометрической тени называется дифракцией. Пусть плоская волна падает на щель в плоском экране АВ. Согласно принципа Гюйгенса-Френеля, каждая точка волнового фронта является источником вторичных волн, причем все эти различные источники когерентны. Огибающая к фронтам волн от вторичных источников дает положение нового фронта волны. Явление дифракции наблюдается при условии соизмеримости препятствий с длинной волны l~d. Все вторичные источники когерентны и распределение интенсивности есть результат интерференции волн, излучаемых вторичными источниками.
Дифракционная решетка состоит из чередующихся прозрачных и непрозрачных полос. Суммарная ширина прозрачной и непрозрачной полосы называется периодом дифракционной решетки d. Пусть на решетку падает плоская волна. Так как l~d, то лучи начинают откланяться от первоначального направления распространения. Щели являются когерентными источниками.
Фотоэффект. Фотоэлектрическим эффектом называется испускание электронов с поверхности металла под действием света. Если к электродам откачанной трубки приложить напряжение, ток по цепи не потечет, так как пространстве между катодом и анодом нет носителей тока. Но при облучении катода световым потоком в цепи появится ток. При увеличении напряжения сила тока растет, все большее число электронов, покинувших катод под действием света, достигает анода. Начиная с некоторого значения напряжения U1 сила тока в цепи не изменяется. Это означает, что все электроны, вышедшие из катода за 1 с, достигают анода. Этот ток Iн называется фототоком насыщения. Он позволяет определить количество электронов, покидающих катод за 1 с. При U, равном нулю, фототок отличен от нуля. Это объясняется тем, что электроны вылетают из металлической пластинки с некоторой скоростью и не нужно создавать электрического поля для того, чтобы они достигали анода. Для того, чтобы фототок был равен нулю, надо создать поле, препятствующие движению электронов к аноду. Разность потенциалов, при которой электроны не достигают анода, называется задерживающим напряжением Uз. Изменение кинематической энергии должно быть равно работе электростатических сил поля, созданного между электродами: qeUз=mv2/2, где qe и Uз < 0.
Различают 2 случая Д. с. — дифракция сферической волны, при которой размер отверстия сравним с размером зоны Френеля, т. е.
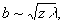
где b — размер отверстия, z — расстояние точки наблюдения от экрана, l — длина волны (дифракция Френеля), и Д. с. в параллельных лучах, при которой отверстие много меньше одной зоны Френеля, т. е.
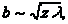
(дифракция Фраунгофера). В последнем случае при падении параллельного пучка света на отверстие пучок становится расходящимся с углом расходимости j ~ l/b (дифракционная расходимость).
Большое практическое значение имеет случай Д. с. на щели. При освещении щели параллельным пучком монохроматического света на экране получается ряд тёмных и светлых полос, быстро убывающих по интенсивности. Если свет падает перпендикулярно к плоскости щели, то полосы расположены симметрично относительно центральной полосы (рис. 3), а освещённость меняется вдоль экрана периодически с изменением j, обращаясь в нуль при углах j, для которых sin j = m/lb (m = 1, 2, 3 ....). При промежуточных значениях освещённость достигает максимальных значений. Главный максимум имеет место при m = 0, при этом sin j = 0, т. е. j = 0. Следующие максимумы, значительно уступающие по величине главному, соответствуют значениям j, определённым из условий: sin j = 1,43 l/b, 2,46 l/b, 3,47 l/b и т.д.
С уменьшением ширины щели центральная светлая полоса расширяется, а при данной ширине щели положение минимумов и максимумов зависит от l, т. е. расстояние между полосами тем больше, чем больше l. Поэтому в случае белого света имеет место совокупность соответствующих картин для разных цветов. При этом главный максимум будет общим для всех l и представится в виде белой полоски, переходящей в цветные полосы с чередованием цветов от фиолетового к красному.
Принцип Г. Обычно для получения изображения какого-либо объекта фотографическим методом пользуются фотоаппаратом, который фиксирует на фотопластинке излучение, рассеиваемое объектом. Каждая точка объекта в этом случае является центром рассеяния падающего света; она посылает в пространство расходящуюся сферическую световую волну, которая фокусируется с помощью объектива в небольшое пятнышко на светочувствительной поверхности фотопластинки. Так как отражательная способность объекта меняется от точки к точке, то интенсивность света, падающего на соответствующие участки фотопластинки, оказывается различной. Поэтому на фотопластинке возникает изображение объекта. Это изображение складывается из получающихся на каждом участке светочувствительной поверхности изображений соответствующих точек объекта. При этом трёхмерные объекты регистрируются в виде плоских двухмерных изображений.
В процессе фотографирования на фотопластинке фиксируется лишь распределение интенсивности, то есть амплитуды электромагнитной волны, отражённой от объекта (интенсивность пропорциональна квадрату амплитуды). Однако световая волна при отражении от объекта изменяет не только амплитуду, но и фазу в соответствии со свойствами поверхности объекта в данной точке.
Г. позволяет получить более полную информацию об объекте, так как представляет собой процесс регистрации на фотопластинке не только амплитуд, но и фаз световых волн, рассеянных объектом. Для этого на фотопластинку одновременно с волной, рассеянной объектом (сигнальная волна), необходимо направить вспомогательную волну, идущую от того же источника света (лазера), с фиксированной амплитудой и фазой (опорная волна, рис. 1).
Интерференционная картина (чередование тёмных и светлых полос или пятен), возникающая в результате взаимодействия сигнальной и опорной волн, содержит полную информацию об амплитуде и фазе сигнальной волны, то есть об объекте. Зафиксированная на светочувствительной поверхности интерференционная картина после проявления называется Голограммой. Если рассматривать голограмму в микроскоп, то в простейшем случае видна система чередующихся светлых и тёмных полос (рис. 2). Интерференционный узор реальных объектов весьма сложен.
[В/м] ; 
; 
- поверхностная плотность заряда
; [Н]
Ф/м
[Дж]
; 
; i – плотность тока
- Электродвиж. сила
[В]
- работа, совершенная сторонними силами
- сила эл. поля
; 
; 
- удельная проводимость.
- температурный кооф. сопр.
- удельное сопротивление
[1 град. ^ -1]
; 
; 
; 
- потенциал эл. поля
- потенциальная энергия заряда в поле.
; 
; 
; 
- магнитная прониц. среды
[Вб]
; 
; 
; 
[Гн]
; 
; W - энергия
; 
; 
- ваакум
; 
; 
;
- относит. показатель преломления.
- скорости света во 2-й и первой средах.
; 
; 
; 
- длинна волны излучения
- импульс фотона
- частота излучения
- относит. диэликтрич. проницаемость среды
- относит. магнитная проницаемость среды.
; 
