|
| X | DX | DX2 | DY | DY | DY2 | DX*DY | | 1 | 70 | -10,4 | 108,9 | 24 | 3,7 | 13,7 | -38,6 | | 2 | 60 | -20,4 | 417,6 | 12 | -8,3 | 69,0 | 169,7 | | 3 | 50 | -30,4 | 926,3 | 18 | -2,3 | 5,3 | 70,1 | | 4 | 30 | -50,4 | 2543,7 | 16 | -4,3 | 18,5 | 217,1 | | 5 | 120 | 39,6 | 1565,4 | 21 | 0,7 | 0,5 | 27,5 | | 6 | 70 | -10,4 | 108,9 | 24 | 3,7 | 13,7 | -38,6 | | 7 | 130 | 49,6 | 2456,7 | 20 | -0,3 | 0,1 | -15,1 | | 8 | 130 | 49,6 | 2456,7 | 34 | 13,7 | 187,6 | 678,8 | | 9 | 90 | 9,6 | 91,5 | 21 | 0,7 | 0,5 | 6,7 | | 10 | 90 | 9,6 | 91,5 | 14 | -6,3 | 39,7 | -60,3 | | 11 | 90 | 9,6 | 91,5 | 28 | 7,7 | 59,2 | 73,6 | | 12 | 85 | 4,6 | 20,8 | 34 | 13,7 | 187,6 | 62,5 | | 13 | 70 | -10,4 | 108,9 | 13 | -7,3 | 53,4 | 76,2 | | 14 | 50 | -30,4 | 926,3 | 18 | -2,3 | 5,3 | 70,1 | | 15 | 75 | -5,4 | 29,5 | 10 | -10,3 | 106,2 | 56,0 | | 16 | 80 | -0,4 | 0,2 | 12 | -8,3 | 69,0 | 3,6 | | 17 | 80 | -0,4 | 0,2 | 12 | -8,3 | 69,0 | 3,6 | | 18 | 75 | -5,4 | 29,5 | 18 | -2,3 | 5,3 | 12,5 | | 19 | 110 | 29,6 | 874,1 | 21 | 0,7 | 0,5 | 20,6 | | 20 | 100 | 19,6 | 382,8 | 24 | 3,7 | 13,7 | 72,3 | | 21 | 55 | -25,4 | 646,9 | 25 | 4,7 | 22,0 | -119,4 | | 22 | 80 | -0,4 | 0,2 | 27 | 6,7 | 44,8 | -2,9 | | 23 | 60 | -20,4 | 417,6 | 21 | 0,7 | 0,5 | -14,2 | | Сумма | 1850 | 0,0 | 14295,7 | 467 | 0,0 | 984,9 | 1332,0 | | | Xср= | 80,43 |
| Yср= | 20,30 | | DX= | 649,80 |
| DY= | 44,77 | | dX= | 25,49 |
| dY= | 6,69 | | VX= | 0,32 |
| VY= | 0,33 | |
|
|
|
|
| | r= | 0,35 | слабая связь | | 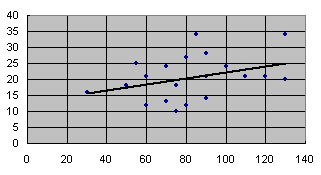
| Вывод: несмотря на то что оба каждый показатель (мощность почв и урожайность трав) коэффициент вариации у них одинаковый (соответственно 0,32 и 0,33). Следовательно по отдельности каждый является средними по однородности. Проведенные вычисления показали, что они находятся в слабой корреляционной связи. Для примера возьмем противоположные данные мощности почв: 120 и 60 см, но урожайность трав у них одинаковая. Урожайность трав зависит от многих факторов и мощность почв в данном поясе не играет большого значения. Возможно в других районах, например черноземном поясе, мощность почв будет более значима и связь будет сильнее. |